円周角の定理とその逆の証明

【目次】
１．円周角の定理
  １－１．証明の方針
  １－２．円周角の定理の証明
２．円周角の定理の逆
  ２－１．証明の方針
  ２－２．円周角の定理の逆の証明

このページでは、円周角の定理とその逆について、詳しい証明を行います。

数学Ａの教科書（数研出版、高校数学の教科書、以下同じ。詳しくは、高校数学マスター基本方針：参考にする教科書を参照ください）では、円周角の定理とその逆は中学で学ぶ事柄の復習として証明なしで紹介されています。

ただ、実際に中学で学んだ時点で詳しい証明を確認したかどうか、証明抜きの事実として用いてきた人も多いのではないでしょうか。円周角の定理とその逆は、円に関係する多くの命題で利用される基礎的な定理なので、一度は確認しておくと良いと思います。

このような基礎的な定理をきちんと自分で証明できる力が付いてくると、教科書を読みこなすことや応用問題を解くことも割と容易になってくるだろうと思います。

円周角の定理

教科書によると、円周角の定理とは、

【円周角の定理】

一つの弧に対する円周角の大きさは一定であり、その弧に対する中心角の大きさの半分である。

という定理です。

証明の方針

【証明の方針】
まず、上記の【円周角の定理】が二つの部分から成立していることに着目しましょう。

つまり、「一つの弧に対する円周角の大きさは一定であること」と「その弧に対する中心角の大きさの半分であること」の二つです。

「一つの弧に対する円周角の大きさは一定であること」は、一つの弧に対する「すべての」円周角の大きさは一定であることを主張しています。それはつまり、直接証明するのであれば、「すべての」円周角の中から、「どの二つの」円周角を取り出してみても、その大きさが一定であることを証明しなければなりません。

一方で、「その弧に対する中心角の大きさの半分であること」については、中心角は一つの弧に対して一つに定まります。したがって、一つの中心角は対して、「すべての」円周角の中から、「一つの」円周角を取り出してみて、その大きさが半分であることを示せば良いことになります。

つまり、前者の方が後者よりも一般性が高く、証明が難しそうなのです。くわえて、後者を示せば、すべての円周角は中心角の大きさの半分なので、すべての中心角の大きさは等しいという前者を示したことにもなります。

よって、【円周角の定理】の証明の方針としては、基本的には後者を示すことにします。

次に、どんな命題でも一度にすべてを証明する方針が思いつかないときは、命題をより単純な事例に分解し、より簡単なことから証明を行うことが大切です。つまり、場合分けをするわけですが、その際に注意することは、すべての場合を網羅して穴がないことを確認することです。（参考：合理的に物事を考える方法：デカルトの真理探究法）

今回の【円周角の定理】については、弧の長さによって円周角が決まるので、弧の長さで場合分けをすることになります。その際に、弧が決まれば、弦も決まることに着目し、弦と円の中心との位置関係にも気を配ると分かりやすいと思います。

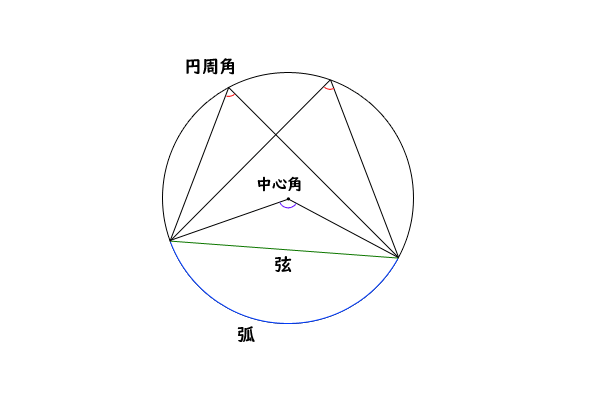
図１：円周角の定理、弧、弦、円周角、中心角

そして、このページで紹介する【円周角の定理】の証明の一番のポイントは、円の半径が一定であることから、二等辺三角形を見つけ出し、円周角を二つの二等辺三角形の底辺の角の大きさの和や差で表せばよいことに気づけるかどうかになります。

それでは、証明に入りたいと思います。

円周角の定理の証明

【証明】
次のように、弧の長さで場合分けし、すべての場合を簡単な場合から証明していきます。

場合①：弧が円周の半分の長さである。

場合②：弧が円周の長さの半分よりも長い。

場合③：弧が円周の長さの半分よりも短い。

さらに、場合③においては、弦と円周角から成る三角形と円の中心との位置関係で二つの場合に分けて証明します。

場合③－①：円の中心が弦と円周角から成る三角形の中にある。

場合③－②：円の中心が弦と円周角から成る三角形の外にある。

以上の場合です。

ここで、円の中心点を\(O\)、弧の端点を\(A\)と\(B\)、円周角の点を\(C\)とします。

それでは、まず、場合①を証明します。

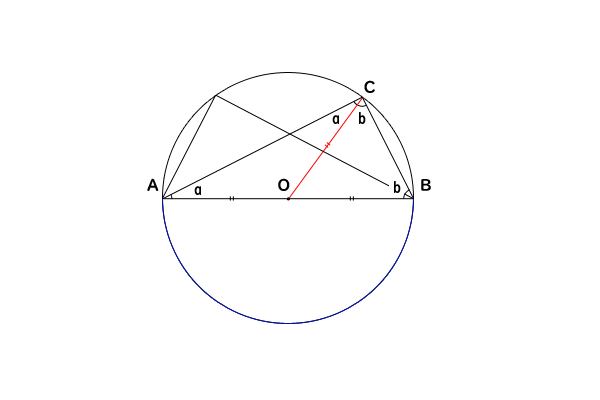
図２：場合① 弧が円周の半分の長さ

弧が円周の半分の長さであるので、弧\(AB\)は半円であり、線分\(AB\)は円の直径となります。したがって、線分\(AB\)は円の中心点\(O\)を通ります。

今、線分\(OC\)を引いて、三角形\(CAB\)を二つの三角形\(CAO\)と三角形\(CBO\)に分けることができます。

ここで、三角形\(CAO\)と三角形\(CBO\)の辺\(AO\)、辺\(CO\)、辺\(BO\)は、すべて円の半径なので長さが等しくなります。

したがって、三角形\(CAO\)と三角形\(CBO\)は二等辺三角形であり、その角について、

\[\angle OAC = \angle OCA, \angle OBC = \angle OCB \]

が成り立ちます。（参考：三角形の辺の長さと角の大きさの関係の証明）

そこで、\(\angle OAC = a, \angle OBC = b \)とおくと、三角形\(CAO\)と三角形\(CBO\)の内角の和について、

\[180^\circ = 2a + \angle AOC \tag{1}\]

\[180^\circ = 2b + \angle BOC \tag{2}\]

が成り立ちます。

さらに、直線上の一点における一方の側の角度は\(180^\circ \)なので、

\[180^\circ = \angle AOC + \angle BOC \tag{3}\]

が成り立つので、式（１）と式（２）の和を取り、式（３）を代入して、式変形すると、

\[360^\circ = 2a + 2b + \angle AOC + \angle BOC = 2a + 2b + 180^\circ \]

\[180^\circ = 2a + 2b\]

\[90^\circ = a + b \tag{4}\]

が分かりました。

ここで、円周角\(\angle ACB = \angle ACO + \angle BCO\)なので、式（４）より、

\[\angle ACB = a + b = 90^\circ\]

であることが分かりました。

一方、中心角\(\angle AOB\)は、直線上の一点における一方の側の角度であり、やはり、\(180^\circ \)なので、円周角が中心角の半分の大きさになることが示せました。

次に場合②：弧が円周の長さの半分よりも長い、を証明します。

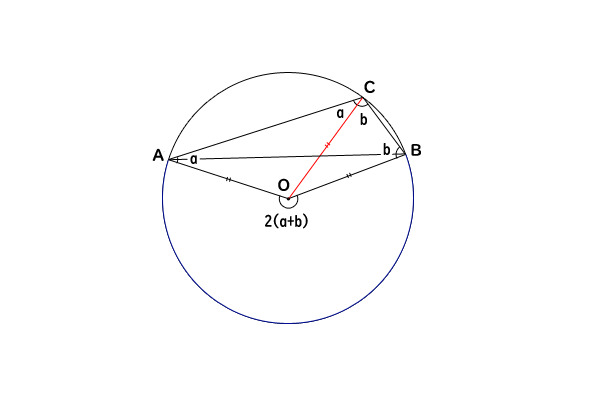
図３：場合② 弧が円周の長さの半分よりも長い

基本的には、場合①と同様で式（１）（２）が成り立ちます。

違いは、\(\angle AOB\)が\(180^\circ\)ではないところです。したがって、中心角の反対側の\(\angle AOB\)について式（３）を、

\[\angle AOB = \angle AOC + \angle BOC \tag{5}\]

と書き直します。

さらに、中心角の角度を\(c\)とすると、

\[c = 360^\circ – \angle AOB \tag{6}\]

なので、式（５）に式（１）（２）（６）を代入して\(\angle AOB\)、\(\angle AOC\)、\(\angle BOC\)を消去すると、

\[360^\circ – c = (180^\circ -2a) + (180^\circ – 2b) \]

\[ c = 2a + 2b = 2 (a + b) = 2 \angle ACB \]

したがって、円周角が中心角の半分の大きさになることが示せました。

次に、場合③－①：円の中心が弦と円周角から成る三角形の中にある、の証明ですが、弧と円の中心点の位置関係は変わりますが、この証明は場合②とまったく同様に行うことができます。

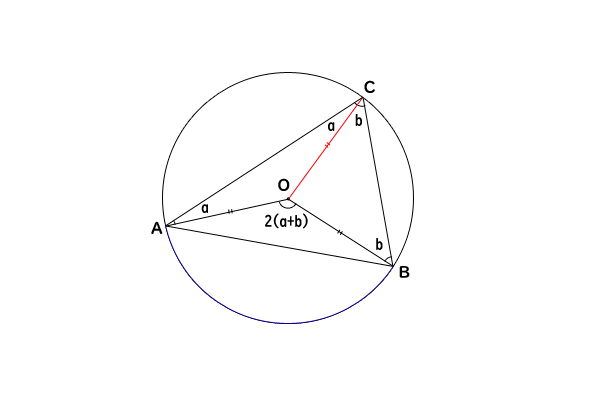
図４：場合③－① 円の中心が弦と円周角から成る三角形の中にある

次に、場合③－②：円の中心が弦と円周角から成る三角形の外にある、の証明をします。

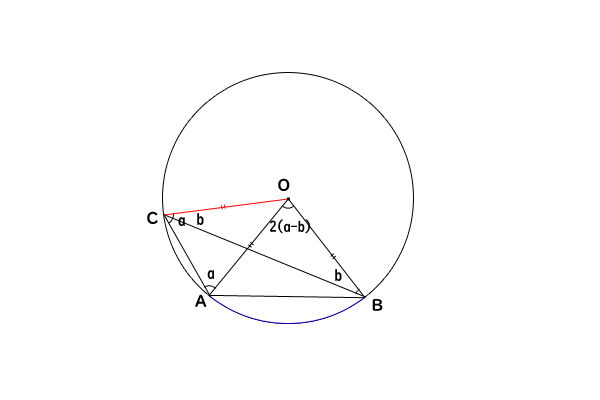
図５：場合③－② 円の中心が弦と円周角から成る三角形の外にある

これまでと同様に、三角形\(OAC\)と三角形\(OBC\)について、\(\angle OAC = a, \angle OBC = b \)とおいて考えます。

そうすると、式（１）（２）についても同様に成り立ちます。

これまでと異なるのは、円周角\(\angle ACB = a + b\)ではなく、

\[\angle ACB = a – b \tag {7}\]

となっているところです。ちなみに、円周角が左右反対の位置にあれば、\(\angle ACB = b – a\)となりますが、証明は同様に成立します。

さらに、中心角について、

\[\angle AOB = \angle BOC – \angle AOC \tag {8}\]

が成り立つので、式（１）（２）（７）を代入して、

\[\angle AOB = (180^\circ – 2b) – (180^\circ – 2a) \]

\[\angle AOB = 2a – 2b = 2( a – b ) = 2 \angle ACB \]

したがって、円周角が中心角の半分の大きさになることが示せました。

これで、すべての弧の長さの場合について、円周角の定理を証明することができました。□

円周角の定理の逆

教科書によると、円周角の定理の逆とは、

【円周角の定理の逆】

四点\(A,B,P,Q\)について、点\(P,Q\)が直線\(AB\)に関して同じ側にあって、

\[\angle APB = \angle AQB\]

ならば、四点\(A,B,P,Q\)は一つの円周上にある。

という定理です。

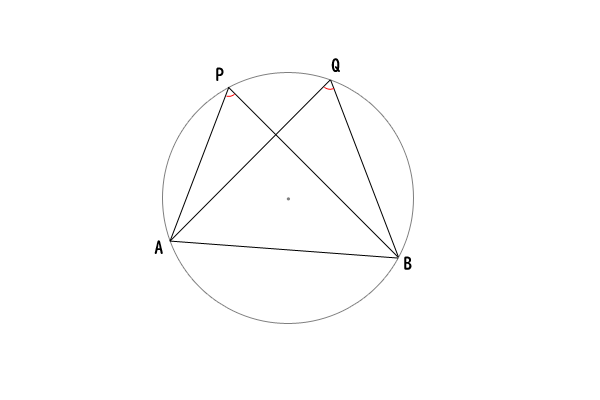
図６：円周角の定理の逆

証明の方針

【証明の方針】

まず、「逆」の意味を説明したいと思います。

【円周角の定理】は、ある円周上の弧が一つ定まると、そのすべての円周角の大きさが等しいという定理でした。

このとき、弧によって一つ定まる弦に注目して、【円周角の定理】を考え直してみます。

つまり、ある円周上の弦が一つ定まると、弦はその円周を二つの弧に分割します。

そこで、その二つの弧について【円周角の定理】の定理が成立するので、【円周角の定理】は、ある円周上の弦が一つ定まると、二つの弧が定まり、その各弧についてすべての円周角の大きさが等しい、と言い換えられます。

さらに、弧についての明示的な言及を無くして、ある円周上の弦が一つ定まると、片側のすべての円周角の大きさが等しい、と言い換えても同じことです。

【円周角の定理の逆】は、この言い換えの逆を意味しています。つまり、どのような線分\(AB\)でも、それを弦とする円を考えたときに、直線\(AB\)の同じ側に、\(\angle APB = \angle AQB\)を満たす点\(P,Q\)があれば、点\(P,Q\)をも通る円が一つに定まるという定理です。

整理すると、線分\(AB\)の片側について、線分\(AB\)を弦とする、ある円において、

【円周角の定理】：円周上に点\(P,Q\)がある \(\Rightarrow\) \(\angle APB = \angle AQB\)

【円周角の定理の逆】：円周上に点\(P,Q\)がある \(\Leftarrow\) \(\angle APB = \angle AQB\)

となります。

ちなみに、以下の証明で、一般に一直線上にない異なる三点を通る円はただ一つのみ存在することが示されるので、【円周角の定理の逆】を満たす円、つまり、四点\(A,B,P,Q\)を通る円が一つしかないことも分かります。

さらに付け加えれば、この定理の前提には、「\(\angle APB \neq \angle AQB\)であれば、点\(P,Q\)を通る円があると【円周角の定理】に矛盾するので、そのような円は存在しない。そして、線分\(AB\)を弦とする円は無数にあるので、【円周角の定理】より、\(\angle APB = \angle AQB\)を満たす点\(P,Q\)について、円周上にあるものが無数に存在していることも分かっている。しかし、\(\angle APB = \angle AQB\)を満たす、すべての点\(P,Q\)について、それを通る円があるのか、さらに一つに定まるのか。」という疑問があるわけです。

そして、その答えが「Yes」なのです。

以下の証明のポイントは、垂直二等分線を引くことと、平行線の錯角を上手く使うことです。

それでは、証明に入りたいと思います。

円周角の定理の逆の証明

【証明】

まず、点\(A\)と点\(B\)の垂直二等分線\(l\)を考えます。

点\(A\)と点\(B\)の垂直二等分線とは、線分\(AB\)の中点を点\(M\)として、点\(M\)を通って線分\(AB\)に垂直な直線を指します。

垂直二等分線\(l\)上の任意の点\(R\)を考えると、三角形\(ARM\)と三角形\(BRM\)について、辺\(RM\)が共通で、\(AM=BM\)であり、\(\angle RMA = \angle RMB = 90^\circ\)であり、二辺挟角が等しいので、三角形\(ARM\)と三角形\(BRM\)は合同であることが分かります。

したがって、\(AR = BR\)が成り立ちます。

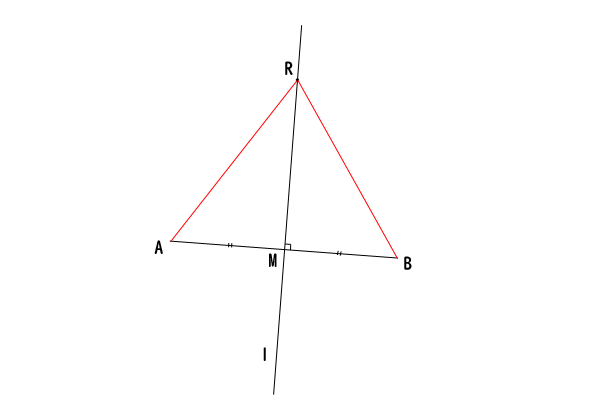
図７：垂直二等分線の二辺

一方、垂直二等分線\(l\)上にない任意の点\(S\)を考えると、仮に\(AS = BS\)が成立すると、三角形\(ASB\)は二等辺三角形になります。

そこで、点\(S\)より線分\(AB\)に向かって\(\angle ASB\)の角の二等分線を引き、線分\(AB\)との交点を点\(M^{‘}\)とすると、三角形\(ASM^{‘}\)と三角形\(ASM^{‘}\)について、辺\(SM^{‘}\)が共通で、\(SA=SB\)であり、\(\angle SM^{‘}A = \angle SM^{‘}B\)であり、二辺挟角が等しいので、三角形\(ASM^{‘}\)と三角形\(ASM^{‘}\)は合同であることが分かります。

したがって、\(AM^{‘}=BM^{‘}\)となります。さらに、\(\angle AM^{‘}S = \angle BM^{‘}S\)かつ\(\angle AM^{‘}S + \angle BM^{‘}S = 180^\circ\)なので、\(\angle AM^{‘}S = \angle BM^{‘}S = 90^\circ\)となり、直線\(SM^{‘}\)は線分\(AB\)の垂直二等分線となるので、これは点\(S\)の取り方と矛盾します。

したがって、\(AS \neq BS\)であることが分かりました。

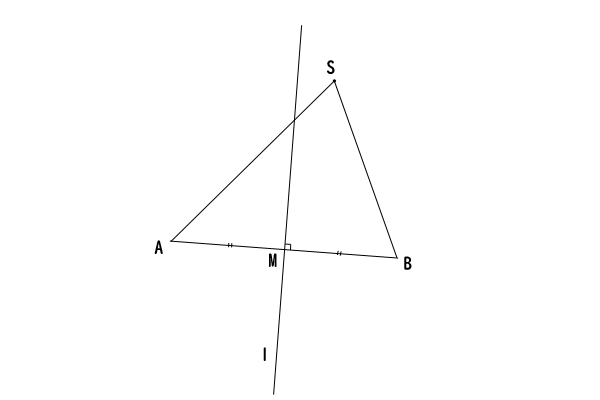
図８：垂直二等分線上にない点

今、点\(A\)と点\(B\)を通る任意の円の中心点を\(C\)とすると、一つの円の半径はすべて等しいので\(AC=BC\)となります。

上述より、点\(A\)と点\(B\)までの長さが等しい点は、垂直二等分線\(l\)上の点であることが分かっているので、点\(A\)と点\(B\)を通る任意の円の中心点は、垂直二等分線\(l\)上の点であり、逆に、垂直二等分線\(l\)上の任意の点は、点\(A\)と点\(B\)を通る一つの円の中心点であることが分かりました。

次に、点\(A\)と点\(P\)の垂直二等分線\(m\)を取ると、同様のことが言えます。

ここで、二直線は、平行であるか、一点で交わるか、全体が重なるか、の三つの場合しかありません。

直線\(l\)と直線\(m\)が平行な場合には、直線\(AB\)と直線\(AP\)は各々の垂線なので、直線\(AB\)と直線\(AP\)が平行か、全体が重なるか、の二つの場合しかありませんが、点\(A\)で二直線は交わっているので、直線\(AB\)と直線\(AP\)は一致することになります。

そうすると、点\(P\)が直線\(AB\)の片側にあるという前提に反するので、この場合は考える必要がないことが分かります。

直線\(l\)と直線\(m\)の全体が重なる場合には、直線\(l\)が垂直二等分線となる任意の二点の組を考えれば、点\(A\)がその片側の点であることが定まれば、もう片方の点は点\(B\)の位置に定まってしまうので、点\(P=B\)となります。

したがって、これも点\(P\)が直線\(AB\)の片側にあるという前提に反するので、この場合も考える必要がないことが分かります。

ゆえに、直線\(l\)と直線\(m\)が一点で交わる場合のみを考えればよいことが分かりました。その交点を点\(C\)とします。

そうすると、先ほど示した通り、点\(A\)と点\(B\)を通る円の中心点は、垂直二等分線\(l\)と一致し、点\(A\)と点\(P\)を通る円の中心点は、垂直二等分線\(m\)と一致しするので、点\(A\)と点\(B\)と点\(P\)を通る円の中心点は、垂直二等分線\(l\)と垂直二等分線\(m\)の交点\(C\)と一致することが分かります。

このことから、点\(A\)と点\(B\)と点\(P\)を通る円が一つしかないことも分かりました。

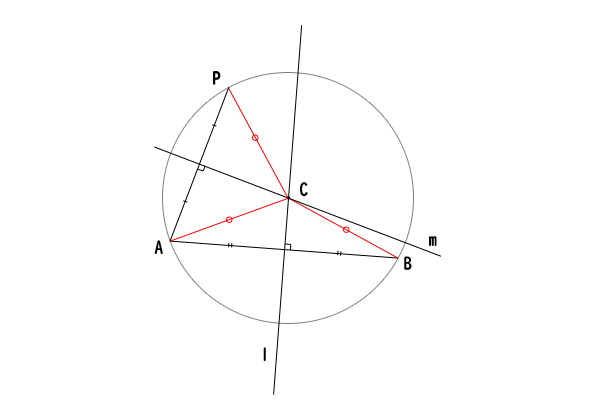
図９：垂直二等分線の交点と外接円

ちなみに、【証明の方針】で触れた通り、以上の証明は、一般に一直線上にない異なる三点を通る円はただ一つのみ存在することを示したことになります。また、一直線上にない異なる三点とは、三角形の頂点でもあるので、三角形の外接円がただ一つのみ存在することと同値です。

それでは、ここで、一つに定まった点\(A\)と点\(B\)と点\(P\)を通る円を円\(O\)とします。

次に、点\(Q\)がこの円\(O\)の円周上にあることを示せれば、四点\(A,B,P,Q\)は一つの円周上にあることが示せたことになります。

ここで仮に、点\(Q\)が円\(O\)の円周上にないとします。

直線\(MQ\)を引くと、点\(M\)は弦\(AB\)の中点なので円\(O\)の内部にあるので、端点\(M\)から伸びる半直線\(MQ\)は、弦\(AB\)に分割された円\(O\)において点\(Q\)と同じ側でその円周と交わることになります。その交点を点\(Q^{‘}\)とします。

点\(Q\)と点\(Q^{‘}\)は異なる点なので、端点\(M\)に対して点\(Q\)は点\(Q^{‘}\)よりも近いか遠いか、同じ側のどちらかにあります。

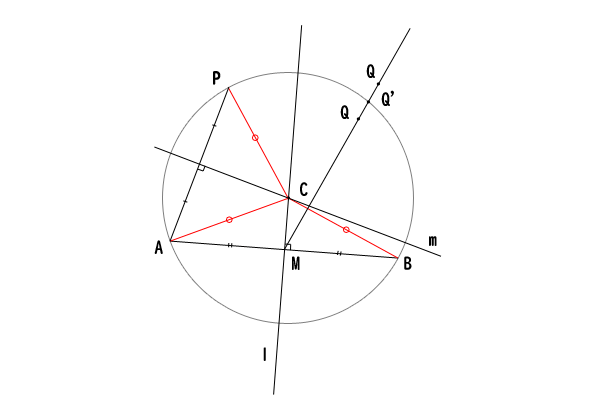
図１０：点Qは近いか、遠いかどちらか

今、直線\(MQ\)は直線\(AB\)と一点\(M\)で交わっていますが、定理の前提より点\(Q\)が直線\(AB\)上にある場合は考える必要がないため直線\(MQ\)と直線\(AB\)が重なる場合は考える必要はありません。したがって、直線\(MQ\)が直線\(AB\)と一点\(M\)のみで交わっている場合のみを考えます。

したがって、点\(A\)は直線\(MQ\)上にないことが分かるので、点\(A\)を通り直線\(MQ\)と平行な直線\(u\)を引くことができます。

そこで、まず、端点\(M\)に対して点\(Q\)が点\(Q^{‘}\)よりも遠い場合、つまり、点\(Q\)が円\(O\)の外部にある場合を考えます。

二直線は、重ならない場合に二点以上で交わることはないので、異なる直線\(u\)、直線\(AQ\)、直線\(AQ^{‘}\)は点\(A\)のみで交わります。したがって、直線\(u\)と直線\(AQ\)のなす角は、直線\(u\)と直線\(AQ^{‘}\)のなす角の内側、つまり、角度は小さくなければなりません。

したがって、平行線の錯角は等しいので、\(\angle AQM \lt \angle AQ^{‘}M\)が成り立ちます。

点\(A\)に対するのと同様に、点\(B\)を通り直線\(MQ\)と平行な直線\(v\)を引くと、\(\angle BQM \lt \angle BQ^{‘}M\)が成り立ちます。

両者を足し合わせると、

\[\angle AQB = \angle AQM + \angle BQM \lt \angle AQ^{‘}M + \angle BQ^{‘}M = \angle AQ^{‘}B\]

\[\angle AQB \lt \angle AQ^{‘}B\]

が成り立ちます。

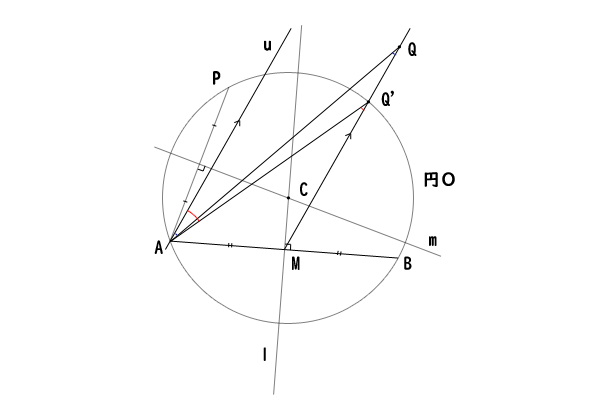
図１１：\(\angle AQM\)が小さい、錯角を用いて

ここで、点\(Q^{‘}\)は円\(O\)の円周上にあるので【円周角の定理】より、\(\angle AQ^{‘}B = \angle APB\)が成り立ちますが、定理の条件\(\angle APB = \angle AQB\)より、\(\angle AQ^{‘}B = \angle AQB\)となり、上式と矛盾します。

次に、端点\(M\)に対して点\(Q\)が点\(Q^{‘}\)よりも近い場合、つまり、点\(Q\)が円\(O\)の内部にある場合を考えると、同様に考えて\(\angle AQB \gt \angle AQ^{‘}B\)が成立するので、やはり、矛盾が生じます。

したがって、点\(Q\)は円\(O\)の円周上にあることが分かりました。□

公開日：２０１９年１０月２４日
修正日：ー