円と直線の距離と位置関係、特に交点、接点、接線について
【目次】
1.交点、接線、接点の定義
2.このページの最終目標
3.前置き:幾何学と論理的思考力
4.点と直線の位置関係
4-1.点と直線についての導入
4-2.垂線の定義、存在、一意性、距離
4-3.点と直線の位置関係、その距離による整理
5.円と直線の位置関係
5-1.円と直線の位置関係、その距離による整理
6.最終目標:二つの命題の証明
このページの目標は、円と直線の位置関係をその距離で整理し、交点、接点、接線についての幾何的な直観によって正しく思える命題を、できるだけ根拠を明示しながらきちんと証明してみせることです。
高校数学の幾何で学ぶべき、幾何的な直観を批判的に吟味してその根拠をさかのぼるという、論理的思考力の基本となる考え方を例示します。
交点、接線、接点の定義
まず、「交点、接線、接点」について考えを少し深めてみましょう。
数学Aの教科書(数研出版、高校数学の教科書、以下同じ。詳しくは、高校数学マスター基本方針:参考にする教科書を参照ください)には、「交点、接線、接点」についての明確な定義は残念ながら書かれていないように思います。
「円と直線」の節で初めて語彙を紹介し、直観的に、円に一点で接する直線のことを接線と呼び、その一点を接点と呼んでいるようです。
一般に解析学においては、接線とは、曲線のある一点について、その一点の近くではその一点のみを共有し、かつ、その一点における傾き(微分係数)が等しい直線のことを指します。そして、その一点を接点と呼びます。
しかし、そのような定義を用いると、例えば四角形が円に内接している場合の共有点を接点と呼ぶことはできません。実際に、教科書はそのような言い回しを避けているようにも感じます。
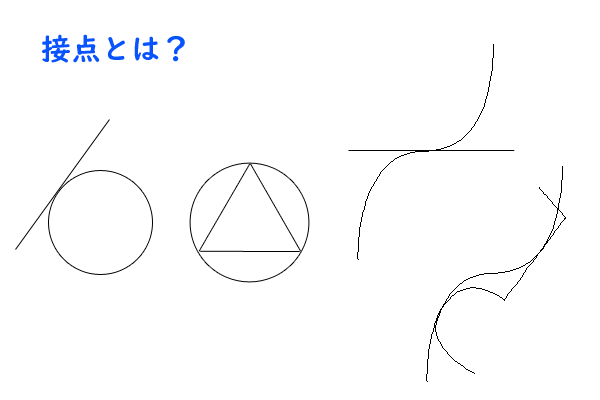
図1:接点とは?
くわえて、例えば\(y=x^{3}\)の原点における接線を考える場合などには、曲線と接線が交差していても接点と呼ばれることになります。接する、触れるという語彙からは少し拡張された定義になるようにも思います。
そこで、このページでは以下のように、念のため直線や円周に限定して「交点、接線、接点」を定義したいと思います。
【定義:交点、接線、接点、接する】
・交点とは、二つの直線や円周のどちらにも含まれる点で、その点を中心とした次の条件を満たす円が存在するものを指す。
交点自身を除いて、円の領域の中に二つの直線や円周のどちらにも含まれる点が存在しない。
特に、以下に定義される接点も交点とする。
・接点とは、交点であり、その点を中心とした次の条件を満たす円が存在するものを指す。
一方の直線や円周によってその円が二分割される、かつ、他方の直線や円周が接点自身を除いてその二分割された領域の一つにしか存在しない。
・接線とは、円周と接点を持つ直線のことである。
・直線が円周に接するとは、その直線が円周の接線になっていることを指す。
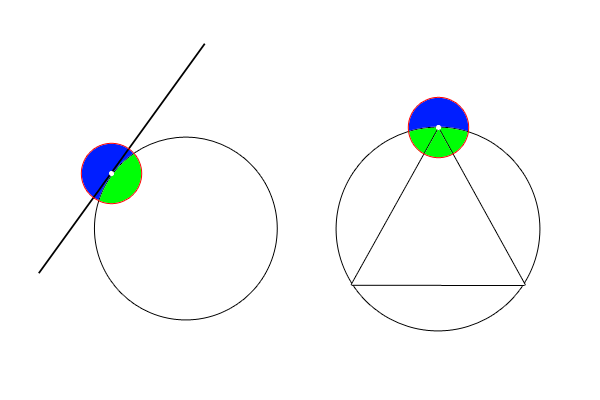
図2:接点の定義
このように定義すれば、もちろん直線や円周への限定の枠内では問題は生じません。そして、たとえ直線や円周への限定を除いて拡張を行ったとしても、高校数学(ユークリッド)の幾何学においては、直観とかけ離れることはなく、大きな問題も生じないと思います。
何より「交点、接線、接点」の理解をより深めることができるのではないかと思います。ただ、前述した通り、解析学における接線、接点の定義とは異なるので、その点は注意してください。例えば、このページの定義のままでは、\(y=0\)は\(y=x^{3}\)の接線にはなりません。
このページの最終目標
とにかくも、このように「交点、接線、接点」を定義した場合に、このページの最終目標は、次の二つの命題を証明することにしたいと思います。
【命題1】
円に接線\(l\)があるとき、円の中心\(O\)とその接点\(A\)を通る直線\(OA\)について、接線\(l\)と直線\(OA\)は垂直に交わる。
【命題2】
逆に、円と交わる直線\(l\)があるとき、円の中心\(O\)とその交点\(A\)を通る直線\(OA\)について、直線\(l\)と直線\(OA\)が垂直に交われば、交点\(A\)は接点であり、直線\(l\)は接線である。
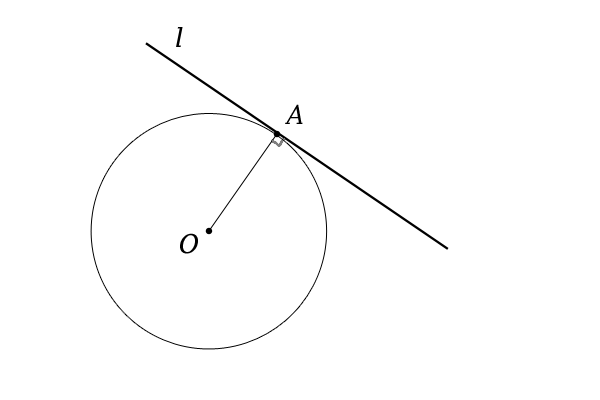
図3:円と接線、垂線
数学Aの教科書によると、同じ内容のことが、
円\(O\)の周上の点\(A\)を通る直線\(l\)について、次のことが成り立つ。
直線\(l\)は点\(A\)で円\(O\)に接する \(\Leftrightarrow\) \(OA \perp l\)
と書かれてありますが、詳しい証明は省かれているので、このページではその証明を示したいと思います。
ちなみに、どうして冒頭で「交点、接線、接点」の定義を明確にしたかというと、この教科書で提示されている命題を証明するためには、「接する」という概念が曖昧過ぎるためです。
つまり、「接する」という概念が曖昧のままでは、この命題は証明のできない前提として受け入れるか、あるいは、「接する」の定義としての役割しか持つことができません。
しかし、この命題の体裁や教科書の文脈からすると、明らかに証明可能な命題として提示されていますので、私は高校生であった頃に頭を悩ませた記憶があります。
この命題を証明可能にするためには、「接する」という概念をその他の前提として受け入れている諸々の事実たちによって再構成し、明確にする必要があるのです。
その際には、「接する」という概念は、「点と線」「交点」「交差」「線の重なり」「線の傾き」「直線と曲線」等々の近い概念と比較され、同じこと、異なること、それをどう表現するかを考えて定義されることになります。実際にそのようにして、冒頭の定義は作成されています。
前置き:幾何学と論理的思考力
一般に昨今の日本の高校数学の教科書は、定理を覚えてその応用ができるようになることを目標としていますので、基本的な定理を証明することや、幾何的な直観を批判的に吟味して、その根拠をさかのぼるという勉強の仕方をほとんど解説していません。
特に、受験を目標とすると、そのような勉強法をさけ、定理を覚えて問題演習を繰り返し、苦手な問題を潰していく、という試験対策の演習に終始してしまいます。試験で点数を取るためであれば、必要な勉強法です。あるいは、特定分野の基礎を身に付けるための正当な訓練法でしょう。
しかし、勉強の大目標は試験で点数を取ることではありませんし、特定分野の基礎を身に付けるためだけでもありません。それは短期的な目標や目標のための必要条件に過ぎず、本当の目標は、将来に直面するだろう予測困難な様々な課題を解決していくことです。
そのためには、個別の知識を身に付ける以上に、より深く原理に近い知識にまで理解を掘り下げること、そのことによって様々な課題に対応できる考える力、合理的に論理的に考える力を身に付けることが大切だと思います。
そして、合理的に論理的に考える力を身に付けるために、その基本となる、物事を批判的に吟味して、その根拠をさかのぼるという考え方を身に付けるために、高校数学で学ぶ幾何は歴史的にも打ってつけの教材と言えるのです。
一度、そのような勉強法、そして、そこで培われる論理的な思考力を身に付ければ、その応用範囲はとても広く、結果として、受験勉強やその後の特定分野の職業訓練等も効率的に進めていくことができるはずです。
はっきり言うと、高校数学の幾何で学ぶべきなのはそこに培われた考え方であって、幾何の知識よりもその考え方の方が、実利的な側面で何十倍も将来の役に立つことになると思います。しかし、残念なことに受験勉強を主目的としがちな日本の高校数学においては、幾何の知識のみを学び、そこに息づく考え方は大急ぎで素通りされます。
結果、数学を学んでも何の役にも立たなかった、という残念な感想しか残りません。
もしも、学生が幾何の一つの問題でも、きちんと時間を取って、批判的に吟味して、その根拠をさかのぼり、議論をしたり、様々な教科書を手に取ったりする、そんな教育を受ければ、その経験は経営でも法律でもどのような仕事でも、その仕事を合理化し、効率化し、良質なものにするための大きな財産となるはずです。
ただ、日本の高校では、学生の学力に合わせてよほど慎重に受験勉強とバランスを取りながらそのようなカリキュラムを作成しないと、何より学生や保護者からの反対に直面することになるかもしれません。
実際に、私の通学していた平均的な学力の高校では、1990年代以前にそのような攻防があったと聞きます。いわく、余計なことをせずに塾と同じ受験勉強を教えろと大変だったそうです。
学生も保護者も目先の受験しか目に入らず、受験範囲をこなすことに精一杯で、範囲外のことはあらゆることを無視し、結局、本当の学力、思考力が伸び悩んでしまうのです。
もちろん、教師の中でもこのような勉強法に価値を見出さないか、反対する人もいます。
少しでも優秀な大学に入ってから勉強すればいいこと、優秀な大学に入らなければ優秀な先生にも友人にも出会えない、基礎知識を身に付ける方が先でそれなしに考える力など育たない、成果を上げた私や彼は中高でそんなことはしなかった、いや今でも知らない、などの意見を耳にするかもしれません。結局、そう思う人はそれで良いのです。
たとえどのような国どのような時代であっても選抜試験は避けられないものです。しかし、若い頃に考える力を身に付けることはそれなりに大切なことです。それぞれに自分の適性や置かれた状況を考慮してバランスを取ることになりますが、あまり目先の結果に一喜一憂せず、無理をせずに楽しみながら努力を続けていくことが最良の選択だろうと思います。
何より勉強は、勉強以上のものではありませんから。
ともあれ、このページは、そのような幾何に息づく考え方の一端をご紹介することを一つの目的としています。そのため、以下で述べられるそれぞれの主張について、どんな疑問への答えなのか、どんな事実を根拠や前提としているか、批判的に吟味して、つまり、疑問を持ちながら探求心を大切にして読んでみてください。
ちなみに、論理的思考力とは何かと疑問に思っている方、あるいは、論理的思考力を身に付けたいという方は、このホームページのトップページをお読みください。
点と直線の位置関係
前置きが長くなりましたが、それでは、解説に入ります。
点と直線についての導入
円と直線の位置関係をその距離で整理するためには、その前に、点と直線の位置関係をその距離で表せる必要があります。
そのためには、点と直線の距離を定義する必要がありますが、まず、点と直線の位置関係は大きく分けて、
【点と直線の位置関係】
点と直線の位置関係は、次のいずれかである。
・直線が点を通る。
・直線が点を通らない。
であることを前提として認めましょう。
次に、点と直線の距離を定義したいのですが、その前に、次の【命題3:点と直線を通る直線】、【命題4:垂線の存在と一意性】、【命題5:垂線と最短距離】を確認します。
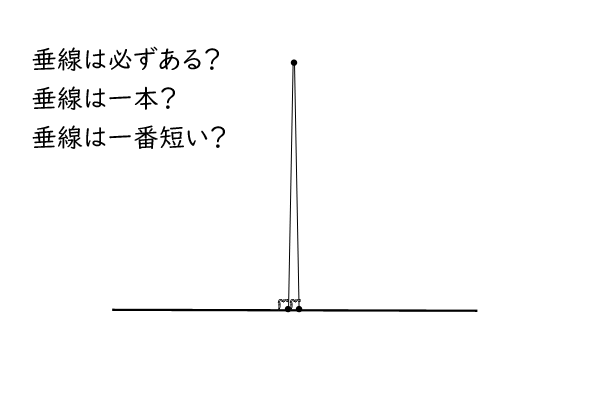
図4:点と直線、垂線に関する疑問
【命題3:点と直線を通る直線】
直線\(l\)が点\(O\)を通らない場合に、点Oと直線\(l\)を通る別の直線\(l^{‘}\)がある。
【証明】
直線\(l\)上の任意の点\(O^{‘}\)が取れることは前提としましょう。
さらに、異なる2点を通る直線が一つあることを前提とすると、点\(O\)と点\(O^{‘}\)は異なる2点なので、直線\(l^{‘}\)が引けることが分かりました。
□
では、直線\(l\)が点\(O\)を通らない場合に、点Oを通るけれど直線\(l\)を通らない別の直線\(l^{‘}\)はあるでしょうか?
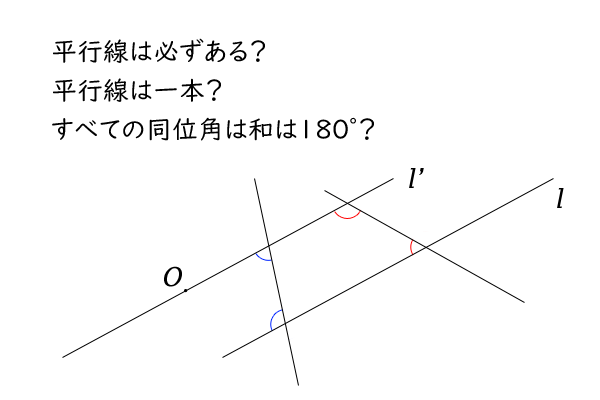
図5:平行線に関する疑問
ありそうですが、私には証明ができそうにないので、あることを前提として、それを平行線と呼ぶことにします。
直観的には、点Oを通って直線\(l\)に平行な直線はただ一つしかなく、くわえて、各直線上の任意の二点を結ぶ線分による同位角の和は常に\(180^\circ\)です。これも証明はできそうにないので、前提としたいと思います。
ただ、平行線に関するこれらの前提は、条件を変えても矛盾を生じないことが知られています。そのような議論、理論を非ユークリッド幾何学と総称し、アインシュタインが物理学に初めて応用したことで有名です。
この前提から、平行線の錯角が等しいことや任意の三角形の内角の和が\(180^\circ\)であることが導かれます。
重要ですが、先を急ぐために簡単な証明に留めますと、
平行線の錯角が等しいことは、一組の平行線の各直線上の任意の二点を線分\(AB\)とすると、線分\(AB\)による同位角の和が\(180^\circ\)であることと、点\(A\)の周りの直線の片側の角度が\(180^\circ\)であること、両者から\(\angle A\)を引くことで導かれます。
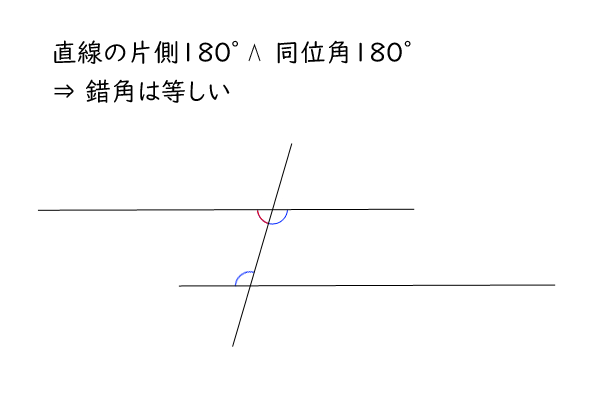
図6:錯角は等しい
任意の三角形\(ABC\)の内角の和が\(180^\circ\)であることは、一辺\(BC\)を底辺として、その対頂角\(A\)を通り底辺\(BC\)に平行な直線を引けば、上記の錯角により、\(\angle A\)と\(\angle B\)と\(\angle C\)の和がその対頂角の周りの直線の片側の角度と等しいことが分かり、かつ、その直線の片側の角度は\(180^\circ\)であることから導かれます。
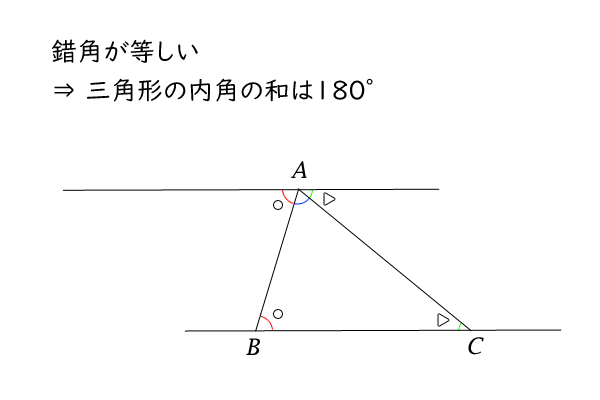
図7:三角形の内角の和
話を戻して、点と直線の距離を定義するための準備を続けたいと思います。
垂線の定義、存在、一意性、距離
そのために重要なのが、次の垂線の定義と【命題4】【命題5】です。
【定義:垂線】
直線\(l\)が点\(O\)を通らない場合に、点\(O\)と直線\(l\)を通る直線\(l^{‘}\)について、
直線\(l\)と直線\(l^{‘}\)が垂直に交わるとき、直線\(l^{‘}\)を点Oから直線\(l\)に下した垂線という。
【命題4:垂線の存在と一意性】
直線\(l\)が点\(O\)を通らない場合に、点\(O\)から直線\(l\)に垂線がただ一つ引ける。
【証明】
前述した平行線の存在の前提より、点\(O\)を通り直線\(l\)に平行な直線\(l^{‘}\)が引けます。
次に、点\(O\)を通り、直線\(l^{‘}\)に垂直な直線\(m\)を引きます。
前述した平行線の一意性の前提より、点\(O\)を通り直線\(l\)に平行な直線はただ一つなので、直線\(m\)は直線\(l\)の平行線ではありません。
したがって、直線\(m\)は直線\(l\)を通ることになります。その交点を点\(O^{‘}\)とします。
そうすると、前述した平行線の同位角の前提より、平行線の同位角の和は\(180^\circ\)で、直線\(m\)は直線\(l^{‘}\)に垂直\(90^\circ\)に交わるので、直線\(m\)は直線\(l\)にも点\(O^{‘}\)において垂直\(90^\circ\)に交わることが分かりました。
したがって、点\(O\)から直線\(l\)への垂線\(m\)が引けました。
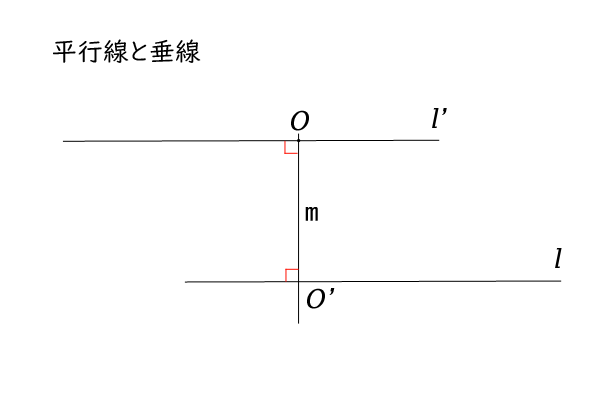
図8:平行線と垂線
さらに、垂線はただ一つであることを示します。
仮に、垂線\(m\)以外に垂線\(m^{‘}\)が引けたとします。
垂線\(m^{‘}\)と直線\(l\)の交点を点\(O^{”}\)とします。
直線は二点によって定まり、垂線\(m\)と垂線\(m^{‘}\)は異なる直線なので、点\(O^{‘}\)と点\(O^{”}\)は直線\(l\)上の異なる点です。
したがって、点\(O\)と点\(O^{‘}\)と点\(O^{”}\)は異なる3点なので、三角形となりますが、\(\angle OO^{‘}O^{”}\)と\(\angle OO^{”}O^{‘}\)は共に\(90^\circ\)であり、\(\angle O^{‘}OO^{”}\)が\(0^\circ\)より大きいので、三角形の内角の和が\(180^\circ\)であることに矛盾します。
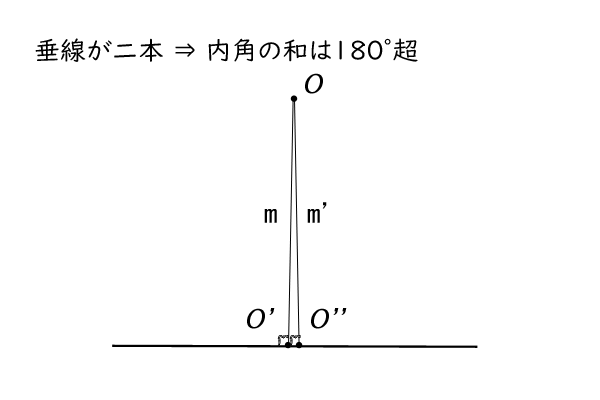
図9:垂線の一意性
したがって、垂線は直線\(m\)以外にはなく、ただ一つであることが示せました。
□
やっと、点と直線の距離を定義するための準備が整ってきました。最後に次の【命題5:垂線と最短距離】を証明しましょう。
【命題5:垂線と最短距離】
直線\(l\)が点\(O\)を通らない場合に、点\(O\)から直線\(l\)に引いた垂線を線分\(OO^{‘}\)とすると、
垂線\(OO^{‘}\)の長さは、点\(O\)と直線\(l\)上の一点を結んで得られるすべての線分おいて、その長さが最も短い。
さらに、点\(O\)と直線\(l\)を結ぶすべての線分おいて、その長さが最も短い線分は、垂線\(OO^{‘}\)のみである。
【証明】
まず、垂線の長さが最も短くなることを示しましょう。
直線\(l\)上の点\(O^{‘}\)とは異なる任意の点\(O^{”}\)を取ります。
そうすると、三角形\(OO^{‘}O^{”}\)において、\(\angle OO^{‘}O^{”}\)が\(90^\circ\)なので、三角形の内角の和は\(180^\circ\)より、\(\angle O^{‘}OO^{”}\)と\(\angle OO^{”}O^{‘}\)の和は\(90^\circ\)になります。
したがって、\(\angle OO^{”}O^{‘}\)は\(90^\circ\)よりも小さくなります。
そうすると、\(\angle OO^{‘}O^{”}\)は\(\angle OO^{”}O^{‘}\)よりも必ず大きいことになりますが、三角形において二つの角の角度の大小とその向かい合う辺の長さの大小は一致するので(参照:三角形の辺の長さと角の大きさの関係)、線分\(O^{‘}O^{”}\)は線分\(OO^{‘}\)よりも必ず長くなることが分かりました。
ちなみに、「三角形の辺の長さと角の大きさの関係」の証明には、【命題4:垂線の存在と一意性】を利用していますが、ここまでで証明が循環していないことも興味があれば確認してみてください。
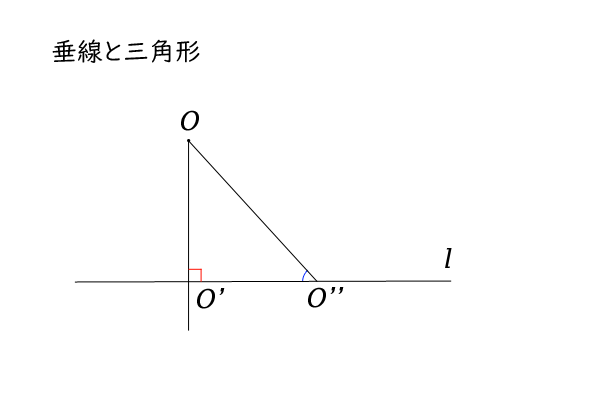
図10:垂線は最も短い、三角形の辺の長さと角の大きさの関係
ともかく、したがって、垂線\(OO^{‘}\)の長さが最も短くなります。
さらに、点\(O^{”}\)は、直線\(l\)上の点\(O^{‘}\)とは異なる任意の点なので、つまり、直線\(l\)上の点\(O^{‘}\)とは異なるすべての点において、上述より、線分\(O^{‘}O^{”}\)は線分\(OO^{‘}\)よりも必ず長くなることが分かるので、長さが最も短い線分は垂線ただ一つであることも分かりました。
□
点と直線の位置関係、その距離による整理
ここでやっと、点と直線の距離を定義することができます。
まず、点と直線の距離とは、位置関係が定まった点と直線の遠近を表す数量であれば良いわけです。
その前提として点と点の距離は、点と点を結ぶ線分の長さで定義されることになります。
一方、点と直線には直線上の各点に複数の線分が引けるので、点と点の距離の定義を援用できる形で、直線上のいずれかの点との線分の長さで点と直線の距離も表したいという動機が生じます。
その上、【命題4:垂線の存在と一意性】によって、垂線はただ一つ存在することが分かり、くわえて、その長さは【命題5:垂線と最短距離】によって、点と直線の間に引かれる線分の中で最も短く、かつ、その長さの線分は垂線以外にないことが分かっています。
したがって、点と直線の距離の妥当な基準として、点と直線に引かれる垂線の長さをその定義として採用することができるわけです。
この点と直線の距離によって、改めてその位置関係を整理することができます。
【点と直線の位置関係、その距離による整理】
点と直線の位置関係は、次のいずれかである。
・直線が点を通る。距離は0である。
・直線が点を通らない。垂線が引けて、その長さが点と直線の距離となり、その距離は0でない。
円と直線の位置関係
さて、それではこの【点と直線の位置関係、その距離による整理】を使って、本題の円と直線の位置関係をその距離で整理していきたいと思います。
今、円\(O\)と直線\(l\)があるとします。
円\(O\)には、中心の点\(C\)があり、半径の長さを\(r\)とします。
【命題4:垂線の存在と一意性】によって、点\(C\)から直線\(l\)への垂線が引けます。これを垂線\(CC^{‘}\)とします。
この垂線\(CC^{‘}\)の長さ、つまり、円\(O\)の中心点\(C\)と直線\(l\)の距離と、円\(O\)の半径の長さ\(r\)の大小関係で、円と直線の位置関係を整理すると、
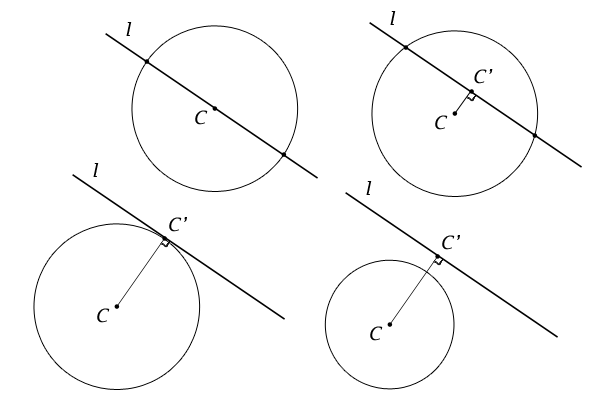
図11:円と直線の位置関係
1.垂線\(CC^{‘}\)の長さが0の場合には、【点と直線の位置関係、その距離による整理】より、直線\(l\)は円\(O\)の中心点\(C\)を通ります。
2.垂線\(CC^{‘}\)の長さが0でない場合で、半径の長さ\(r\)より短いときには、円\(O\)の中心点\(C\)から半径の長さ\(r\)より小さい距離にある点は円の内部にあるので、点\(C^{‘}\)は円\(O\)の内部にあることが分かります。
くわえて、円の内部に端点を持つ半直線は必ず円の外に出ること、直線はそれ自身とは交点を持たないこと、を前提とすると、直線\(l\)は点\(C^{‘}\)を端点として両側の半直線において円\(O\)と異なる交点を持つことになります。
したがって、円\(O\)と直線\(l\)は、少なくとも2つの交点を持つことになります。
それでは、直線\(l\)が円\(O\)の外側に出た後に、さらに別の点で交わることは決してないのでしょうか?
仮に、その一つの交点を点\(A\)とし、点\(A\)を端点として点\(C^{‘}\)の側ではない半直線上に円\(O\)との交点\(B\)があったとすると、三角形\(CC^{‘}A\)と三角形\(CC^{‘}B\)は直角三角形であり、線分\(CC^{‘}\)が共通で、線分\(C^{‘}A\)よりも線分\(C^{‘}B\)の方が大きいので、三平方の定理より、その斜辺\(CA\)よりも斜辺\(CB\)の方が大きいことが分かります。
そうすると、線分\(CA\)は円\(O\)の半径なので、線分\(CB\)は半径の長さ\(r\)よりも長いことになりますが、これは点\(B\)が円\(O\)との交点であることに矛盾します。
したがって、円\(O\)と直線\(l\)は、3つ以上の交点を持たないので、2つの交点を持つことが分かりました。
3.垂線\(CC^{‘}\)の長さが0でない場合で、半径の長さ\(r\)と同じときには、少なくとも点\(C^{‘}\)は、線分\(CC^{‘}\)はその長さが\(r\)で半径となっているので、円\(O\)上にあります。
それでは、やはり直線\(l\)が円\(O\)の外側に出た後に、さらに別の点で交わることは決してないのでしょうか?
仮に、円\(O\)と直線\(l\)が点\(C^{‘}\)と異なる点\(C^{”}\)と交わるとすると、線分\(CC^{”}\)の長さも円\(O\)の半径なので長さ\(r\)となり、点\(C\)から直線\(l\)に対して、垂線と同じ長さの異なる点が引けることになり、【命題5:垂線と最短距離】に反することになります。
したがって、円\(O\)と直線\(l\)は、垂線\(CC^{‘}\)の端点である点\(C^{‘}\)の一点のみにて交わることが分かりました。
4.垂線\(CC^{‘}\)の長さが0でない場合で、半径の長さ\(r\)より長いときには、仮に交点\(C^{”}\)があるとすると、少なくとも点\(C\)と直線\(l\)の距離は半径の長さ\(r\)以下であることになります。つまり、最短距離である垂線\(CC^{‘}\)の長さが\(r\)以下であることになり矛盾します。
したがって、交点は一つもないことになります。
以上を簡単に整理すると、以下のようになります。
円と直線の位置関係、その距離による整理
【円と直線の位置関係、その距離による整理】
円と直線の位置関係は、次のいずれかである。
・円\(O\)の中心点\(C\)と直線\(l\)の距離が半径の長さ\(r\)より短いとき、交点は2つである。
・円\(O\)の中心点\(C\)と直線\(l\)の距離が半径の長さ\(r\)と等しいとき、交点は1つであり、
それを交点\(C^{‘}\)とすると、線分\(CC^{‘}\)は中心点\(C\)から直線\(l\)への垂線である。
・円\(O\)の中心点\(C\)と直線\(l\)の距離が半径の長さ\(r\)より長いとき、交点はない。
最終目標:二つの命題の証明
それでは、この【円と直線の位置関係、その距離による整理】を使って、冒頭で紹介した【命題1】と【命題2】を証明しましょう。
ちなみに、アルファベット\(O\)が指し示す対象が以下では、円ではなく円の中心となるのでご注意ください。
【命題1】
円に接線\(l\)があるとき、円の中心\(O\)とその接点\(A\)を通る直線\(OA\)について、接線\(l\)と直線\(OA\)は垂直に交わる。
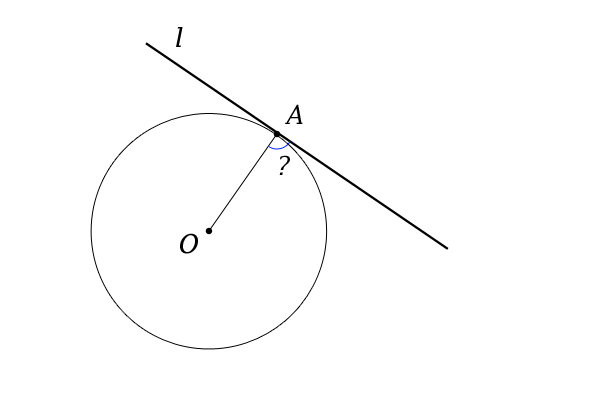
図12:接線の角度
【証明】
ここで、まず冒頭の接線の定義において、接線が円周と一点で交わるとは定義されていないことを確認しておきましょう。つまり、あくまでも、接点を少なくとも一つ持てば接線になるわけです。
したがって、まず、接線が円周と一点で交わることを証明したいと思います。
仮に、円と接線\(l\)が2点で交わるとすると、【円と直線の位置関係、その距離による整理】より、円の中心\(O\)と直線\(l\)の距離が半径の長さ\(r\)より短くなります。
したがって、点\(O\)から直線\(l\)へ垂線\(OO^{‘}\)を引くと、点\(O^{‘}\)は円の内部にあることになります。
そうすると、先ほどの議論と同様ですが、円の内部に端点を持つ半直線は必ず円の外に出ること、直線はそれ自身とは交点を持たないこと、を前提とすると、点\(O^{‘}\)を端点として、その両側の半直線において円と異なる二つの交点を持つことになります。
したがって、接点\(A\)はそのどちらかの点になりますが、どちらにせよ半直線\(O^{‘}A\)は接点\(A\)において円の内部から外部に出ることになります。
そうすると、これは冒頭の接点の定義に定められた条件の円を取ることができないので、点\(A\)は接点ではなくなり矛盾します。
したがって、円と直線\(l\)は、接点\(A\)の一点のみで交わることが分かりました。
【円と直線の位置関係、その距離による整理】より、円と直線が一点のみで交わるのは、中心点\(O\)と直線\(l\)の距離が半径の長さ\(r\)と等しい場合のみであり、そのとき線分\(OA\)は直線\(l\)への垂線であることが分かっています。
□
【命題2】
逆に、円と交わる直線\(l\)があるとき、円の中心\(O\)とその交点\(A\)を通る直線\(OA\)について、直線\(l\)と直線\(OA\)が垂直に交われば、交点\(A\)は接点であり、直線\(l\)は接線である。
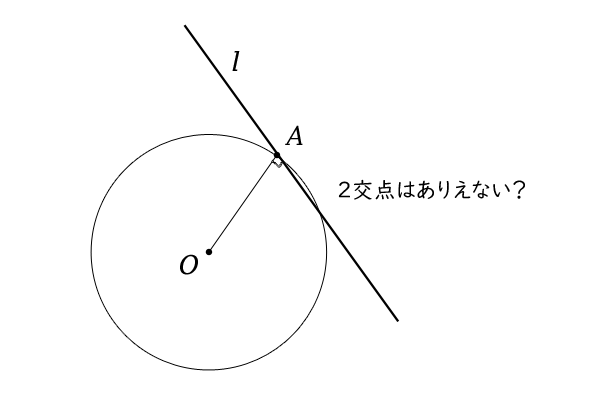
図13:円と接線の交点
【証明】
直線\(l\)と直線\(OA\)が垂直に交わるので、線分\(OA\)は中心\(O\)から直線\(l\)への垂線であり、中心点\(O\)と直線\(l\)の距離は半径の長さ\(r\)と等しくなります。
したがって、【円と直線の位置関係、その距離による整理】より交点は交点\(A\)の一点のみとなります。
くわえて、【命題5:垂線と最短距離】より直線\(l\)上の点\(A\)を除く任意の点\(B\)について、線分\(OB\)は半径の長さ\(r\)よりも長くなるので、点\(B\)は円の外部にあることが分かります。
したがって、点\(A\)を中心とする例えば半径の長さが\(r\)以下の円を取れば、点\(A\)を除いて直線\(l\)上の点は元の円の外部の領域にしかないので、冒頭の接点の定義を満たすことになります。
よって、点\(A\)は接点であり、直線\(l\)は接線となります。
□
著者:L&M個別オンライン教室 瀬端隼也
公開日:2019年10月9日
修正日:ー



※このサイトはreCAPTCHAによって保護されています。そのためGoogleのPrivacy PolicyとTerms of Serviceが適用されます。