複素数の積が0ならば、いずれかは0である代数的証明
【目次】
0.はじめに
1.複素数の積が0ならば、いずれかは0であること
1-1.複素数の積が0ならば、いずれかは0であることの解説
1-2.複素数の積が0ならば、いずれかは0であることの証明
2.平方根が二つだけであること
2-1.平方根の定義
2-2.「ある」「ない」「対応(どうある)」「表す」とは
2-3.他に平方根がないこと
3.根号の乗法と除法における注意点
4.おまけ:教科書の各章冒頭コラムについて
はじめに
このページでは複素数の積\(\alpha \cdot \beta\)が\(0\)ならば、\(\alpha = 0\)または\(\beta = 0\)であることの証明を行います。この命題は、高校数学の教科書(数研出版、高校数学の教科書、以下同じ。詳しくは、高校数学マスター基本方針:参考にする教科書を参照ください)の数学Ⅱ単元「複素数と方程式」の節「複素数」で証明なしで紹介されています。また、この命題を用いて複素数の平方根は多くても二つしかないことを示し、さらに複素数に関わる根号の計算の注意点も示したいと思います。
それでは早速、初めの命題の解説と証明に入りたいと思います。
複素数の積が0ならば、いずれかは0であること
高校数学の教科書には、次のように命題が証明抜きで紹介されています。
「\(\alpha,\ \beta\)を複素数とすると、実数の場合と同様に、次のことが成り立つ。
\(\alpha\beta=0\)ならば\(\alpha=0\)または\(\beta=0\)」
複素数の積が0ならば、いずれかは0であることの解説
まず、「実数の場合と同様に」とありますので、実数の場合を考えてみましょう。
「\(a,\ b\)を実数とすると、次のことが成り立つ。\(ab=0\)ならば\(a=0\)または\(b=0\)」
となります。当たり前のようですが、何となくで納得してしまってはいけません。具体的に根拠を考えて証明してみることが大切です。細かく考えるには対偶を取りましょう。
対偶:「\(a\neq 0\)かつ\(b\neq 0\)ならば\(ab \neq 0\)」
と上記の命題が対偶で、対偶な命題は同値なのでした(参考:対偶の証明について)。ここで、まず\(a\)と\(b\)が共に正の数の場合のみについて、さらに\(a\)を場合分けして考えてみましょう。
\(a\)は\(a\neq 0\)なので、\(1 > a > 0\)、\(a \geq 1\)の場合しかありません。\(1 > a > 0\)のとき、\(ab\)は\(b\)よりも小さくはなりますが\(b\neq 0\)なので\(0\)にはなりません。\(a \geq 1\)のとき、\(ab\)は\(b\)に等しいか大きくはなりますが\(b\neq 0\)なので\(0\)にはなりません。したがって、\(a\)と\(b\)が共に正の数の場合には、\(ab\)は\(0\)にはなりません。
大小関係は異なりますが、\(a\)と\(b\)が共に正の数ではない場合も同様に考えられます。したがって、上記対偶が成り立つことが分かります。つまり、同値である元の命題が正しいことが分かりました。
ここで大事なことは、実数の場合のこの証明には、「\(0\)でない実数を\(0\)でない実数に掛けてもその大きさが大きくなったり小さくなったりはするものの、\(0\)には決してならない」という実数、特に有理数の性質を利用していることにあります。しかしながら、複素数自体には大小関係がなく、大小を直接比較することはできないので、このような証明を同じ形で援用することはできないことになります。
実際に、\(\alpha=a+bi\)、\(\beta=c+di\)とおくと、
\[(a+bi)(c+di)=(ac-bd)+(ad+bc)i\]
となるので、
\[\alpha\beta=0 \Leftrightarrow ac-bd=0 かつ ad+bc=0\]
であり、また、
\[\alpha=0または\beta=0 \Leftrightarrow (a=0 かつ b=0) または (c=0 かつ d=0)\]
なので、つまり、下記を示さなければならず、
\[ac-bd=0 かつ ad+bc=0 \Rightarrow (a=0 かつ b=0) または (c=0 かつ d=0) ①\]
前者から後者を導くのに大小を直接比較すると言っても、どれとどれを比較すれば良いのか容易には分からず、また自明とも言い難いように思います。
一方で、前述の実数の場合の証明で、何でこんな面倒に考えるのだろうと思われた方も中にはいると思いますが、実数の場合は数と図形とを対応させて考えれば、証明すらいらずに自明と言っても良いかもしれません。同様に、複素数を数学Ⅲで学ぶ単元「複素数平面」で考えればこの命題は簡単に正しいと理解することができます。
その図形的な理解を明確にすると、それは極形式による積を用いて、絶対値\(|\alpha\beta|=|\alpha||\beta|\)を導くことができることによります。つまり、
\[\alpha\beta=0 \Rightarrow |\alpha\beta|=0 \Rightarrow |\alpha||\beta|=0 \Rightarrow |\alpha|=0 または |\beta|=0 \Rightarrow \alpha=0 または \beta=0\]
となります。結局、三番目の推論\(\Rightarrow\)に実数の場合を用いているわけです。教科書としても数学Ⅲまで進んでからここに戻ってくればいい、という気持ちで①の証明を省略しているものと思います。
ただ、①は極形式や絶対値や複素平面を学ばなくとも、単純に代数的に証明を行うことができます。少し証明が長いことと、論理的な考察力が必要なために省略されているだけだと思います。そこで、このページではきちんとその代数的な証明を以下で示したいと思います。
ちなみに、この命題が複素数でも成り立つことがなぜ重要かというと、特に後ほど解説する「平方根が二つだけであること」の証明にこの命題が必要になるからです。この命題は実数、複素数では成り立ちますが、一般に積が定義されているからといって必ずしも成り立つとは限らない法則になります。
例えば、一昔前まで、高校数学でも教えられていた行列では必ずしも成立しません。つまり、この命題は実数や複素数を特徴づけるそれなりに厳しい条件であると言えるのです。と言うのは、この命題が成り立たなければ因数分解ができても、すべての根がその因数分解の因数に表れているとは言えなくなるからです。逆に言えば、この命題によってすべての根が因数分解の因数に限られることが主張できることになります。
このことは、後ほど解説する「平方根が二つだけであること」の証明で再度、詳しく触れたいと思います。
複素数の積が0ならば、いずれかは0であることの代数的証明
【複素数の積が0ならば、いずれかは0であることの代数的証明】
背理法を用いて証明したいと思います。つまり、
\(\alpha\beta=0\)ならば\(\alpha=0\)または\(\beta=0\)
を証明したいので、結論「\(\alpha=0\)または\(\beta=0\)」の否定である「\(\alpha \neq 0\)かつ\(\beta \neq 0\)」を仮定して、上記命題の仮定である「\(\alpha\beta=0\)」から推論をして両者の矛盾を導き出します。
まず、解説で説明した通り、
\[\alpha\beta=0 \Leftrightarrow ac-bd=0 かつ ad+bc=0 ②\]
が成り立ちます。一方で、
\[\alpha \neq 0 \Leftrightarrow a\neq 0 または b\neq 0\]
と
\[\beta \neq 0 \Leftrightarrow c\neq 0 または d\neq 0\]
も成り立つので、「\(\alpha \neq 0\)かつ\(\beta \neq 0\)」であるならば、次の4つのいずれかは必ず成り立ちます。
〈1〉\(a\neq 0\)かつ\(c\neq 0\)
〈2〉\(a\neq 0\)かつ\(d\neq 0\)
〈3〉\(b\neq 0\)かつ\(c\neq 0\)
〈4〉\(b\neq 0\)かつ\(d\neq 0\)
したがって、この〈1〉~〈4〉の場合に、いずれにおいても矛盾が導き出されることを示せば、「\(\alpha \neq 0\)かつ\(\beta \neq 0\)」を仮定すると矛盾が生じることを示すことができたことになります。
それでは、まず〈1〉\(a\neq 0\)かつ\(c\neq 0\)の場合を考えると、\(a\neq 0\)かつ\(c\neq 0\)なので前述の実数の場合で示した通り\(ac\neq 0\)が成り立ちます。②より\(ac-bd=0\)、したがって、\(ac=bd\)なので、\(bd \neq 0\)も分かりました。
②より\(ad+bc=0\)でもあるので、\(ad=-bc\)であり、両辺を\(ac\neq 0\)かつ\(bd \neq 0\)より\(ac=bd\)で割ることができ、
\[\frac{ad}{ac}=\frac{-bc}{bd}\]
が成り立ち、したがって、
\[\frac{d}{c}=\frac{-c}{d} \Rightarrow d^2=-c^2\]
が成り立ちます。
一方で、\(c\neq 0\)です。また\(bd \neq 0\)なので、仮に\(d = 0\)とすると\(bd = 0\)で矛盾するので\(d\neq 0\)であることが分かります。そうすると、\(c\)と\(d\)は実数なので\(c^2 > 0\)かつ\(d^2 > 0\)が成り立ち、\(-c^2 < 0\)になるはずです。そうすると、\(d^2 > 0\)は正の数であり、\(-c^2 < 0\)は負の数となり\(d^2 \neq -c^2\)が成り立ちます。つまり、\(d^2=-c^2\)の等号は成り立ちません。
よって、\(d^2=-c^2\)の真偽共に示すことができてしまったので、〈1〉\(a\neq 0\)かつ\(c\neq 0\)の場合の矛盾を導くことができました。
〈2〉~〈4〉も多くの議論が同様なので、〈1〉ほど詳しく記述しませんが次の通りになります。
〈2〉\(a\neq 0\)かつ\(d\neq 0\)の場合を考えると、\(a\neq 0\)かつ\(d\neq 0\)なので\(ad\neq 0\)が成り立ちます。②より\(ad+bc=0\)、したがって、\(ad=-bc\)なので、\(-bc \neq 0\)も分かりました。
②より\(ac-bd=0\)でもあるので、\(ac=bd\)であり、両辺を\(ad\neq 0\)かつ\(-bc \neq 0\)より\(ad=-bc\)で割ることができ、
\[\frac{ac}{ad}=\frac{bd}{-bc}\]
が成り立ち、したがって、
\[\frac{c}{d}=\frac{d}{-c} \Rightarrow c^2=-d^2\]
が成り立ちます。
一方で、\(d\neq 0\)です。また\(-bc \neq 0\)なので、\(c\neq 0\)であることが分かります。そうすると、\(c^2 > 0\)は正の数であり、\(-d^2 < 0\)は負の数となり\(c^2 \neq -d^2\)が成り立ちます。つまり、\(c^2=-d^2\)の等号は成り立ちません。
よって、\(c^2=-d^2\)の真偽共に示すことができてしまったので、〈2〉\(a\neq 0\)かつ\(d\neq 0\)の場合の矛盾を導くことができました。
〈3〉\(b\neq 0\)かつ\(c\neq 0\)の場合を考えると、\(b\neq 0\)かつ\(c\neq 0\)なので\(bc\neq 0\)が成り立ちます。②より\(ad+bc=0\)、したがって、\(ad=-bc\)なので、\(ad \neq 0\)も分かりました。
②より\(ac-bd=0\)でもあるので、\(ac=bd\)であり、両辺を\(ad\neq 0\)かつ\(bc \neq 0\)より\(ad=-bc\)で割ることができ、
\[\frac{ac}{ad}=\frac{bd}{-bc}\]
が成り立ち、したがって、
\[\frac{c}{d}=\frac{d}{-c} \Rightarrow c^2=-d^2\]
が成り立ちます。
一方で、\(d\neq 0\)です。また\(-bc \neq 0\)なので、\(c\neq 0\)であることが分かります。そうすると、\(c^2 > 0\)は正の数であり、\(-d^2 < 0\)は負の数となり\(c^2 \neq -d^2\)が成り立ちます。つまり、\(c^2=-d^2\)の等号は成り立ちません。
よって、\(c^2=-d^2\)の真偽共に示すことができてしまったので、〈3〉\(b\neq 0\)かつ\(c\neq 0\)の場合の矛盾を導くことができました。
〈4〉\(b\neq 0\)かつ\(d\neq 0\)の場合を考えると、\(b\neq 0\)かつ\(d\neq 0\)なので\(bd\neq 0\)が成り立ちます。②より\(ac-bd=0\)、したがって、\(ac=bd\)なので、\(ac \neq 0\)も分かりました。
②より\(ad+bc=0\)でもあるので、\(ad=-bc\)であり、両辺を\(ac\neq 0\)かつ\( bd\neq 0\)より\(ac=bd\)で割ることができ、
\[\frac{ad}{ac}=\frac{-bc}{bd}\]
が成り立ち、したがって、
\[\frac{d}{c}=\frac{-c}{d} \Rightarrow d^2=-c^2\]
が成り立ちます。
一方で、\(d\neq 0\)です。また\(ac \neq 0\)なので、\(c\neq 0\)であることが分かります。そうすると、\(d^2 > 0\)は正の数であり、\(-c^2 < 0\)は負の数となり\(d^2 \neq -c^2\)が成り立ちます。つまり、\(d^2=-c^2\)の等号は成り立ちません。
よって、\(d^2=-c^2\)の真偽共に示すことができてしまったので、〈4〉\(b\neq 0\)かつ\(d\neq 0\)の場合の矛盾を導くことができました。
以上で、〈1〉~〈4〉の場合のいずれにおいても矛盾が導き出されることが分かりました。したがって、「\(\alpha \neq 0\)かつ\(\beta \neq 0\)」を仮定すると矛盾が生じるので、結論「\(\alpha=0\)または\(\beta=0\)」が成り立たなければならないことが分かりました。□
平方根が二つだけであること
このサイトで参照している高校数学の教科書では、上記命題【複素数の積が0ならば、いずれかは0であること】を紹介した後に、この次の命題「平方根が二つだけであること」を紹介しています。この順序を見たときに著者らの若干の苦しみと高校生諸氏がより深い学びを探究してくれることへの淡い希望を伺わせる、と感じるのが妥当なのだろうと思います。
高校数学の教科書は、様々な学生が学ぶ入門書であり、また多くの制約があります。本来ならば、【複素数の積が0ならば、いずれかは0であること】を証明し、この命題を用いて次の命題「平方根が二つだけであること」を証明・解説するところなのですが、どちらも紹介に留めているわけです。私としては知識の量よりも質、どんな生徒であってもゆっくりと解説した方が将来に繋がると思いますが、なかなか日本の現状の教育では難しい点があるのだろうと思います。
平方根の定義
以下、高校数学の教科書と重なる点もありますが、実数\(a\)の平方根を考えたいと思います。実数\(a\)の平方根とは、ある数\(x\)で\(x\)を二乗すると\(a\)になる、そのような数\(x\)のことを指します。つまり、\(a = x^2\)を満たす、すべての数\(x\)を実数\(a\)の平方根と呼びます。では、\(x\)はどのような数なのか、すべて知りたいと思うわけです。
まず、実数\(a\)を場合分けして考えましょう。実数\(a\)は正の数、\(0\)、負の数の3通りに分けられます。
実数\(a\)が正の数の場合には、数学Ⅰの単元「数と式」の節「実数」で\(a\)の平方根には正と負の二つがあり、その正の平方根を\(\sqrt{a}\)と表すと紹介されています。ただ、これも結果の紹介であって、すべての正の実数\(a > 0\)に平方根があることの証明は紹介されていません。
実際に、厳密な証明は大学の範囲でないと難しいと思いますが、例えば、下記の図のように、正の実数の範囲において二次関数の逆関数が平方根の値となっていることを考えれば、二次関数の連続性よりすべての正の実数\(a > 0\)に正と負の平方根があることは、納得はできるのではないかと思います。あと、数学Ⅰの教科書の課題学習には近似値を求めるための開平法も解説されています。
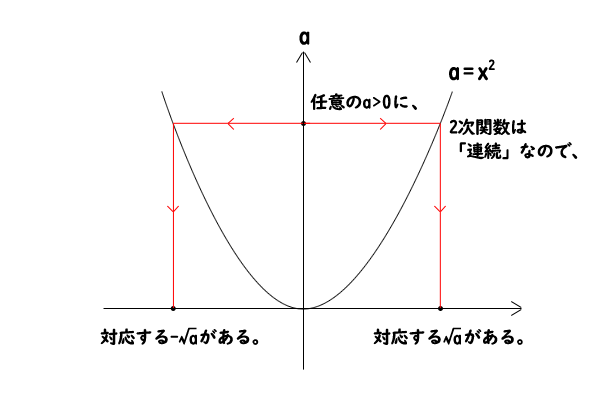
図1:二次関数、\(a\)軸上の正の実数のどの点にも対応する\(\pm\sqrt{a}\)がある。
「ある」「ない」「対応(どうある)」「表す」とは
ちなみに、「ある」という言葉はとても難しい言葉です。例えば、自然数は「ある」と考えている人は多いと思いますが、物の数え方を知らない人からすれば「ない」はずで、同様に、虚数\(i\)は、二乗をすると\(-1\)になるという計算を知っている人からすると「ある」のですが、その計算を理解していない人からすると「ない」のです。
もちろん、この場合の「ない」は「知らない」、「理解できない」と言った方が良いのですが、ただ逆に、ここから分かることは、自然数の「ある」も複素数の「ある」も目に見えてあれ、これと言えるものではなく、物事の理解に依存して成立している概念ということです。同じく「ない」であっても、方程式の解が「ない」というときは、物事の理解に依存した「存在しない」でしょう。これらのことは、\(0\)、負の数、無理数などの概念が「ある」ということについても同様に考えることができます。(物事の理解とは何か、という点については高校数学の範囲を超えると思いますので、ヒントとして合理的に物事を考える方法や論理とは何か、命題、集合と推論規則についてを参考にしてください。)
そして、自然数であれば点や物の個数と「対応」し、無理数であれば線の長さや物の量と「対応」するように、どのように「ある」のか、つまり、何と「対応」を持つのかがその概念の価値と言えるかもしれません。さらに、その概念を既存の概念を用いて「表す」ことができるのかが問題になります。\(0\)や虚数\(i\)はまったくできないので新しい記号が用いられ、負の数は正の数に\(-\)という新しい記号を導入して、無理数は少数点表示で近似はできますが、書き表すことはできないので、特に平方根については\(\sqrt{\ }\)という記号が導入されました。
話が逸れましたが何にせよ、実数\(a\)が正の数の場合には、\(\pm\sqrt{a}\)(と「表さ」れた数)が少なくとも平方根として「ある」ということです。
「少なくとも」と言うのは、ここまで平方根がある、具体的に\(\pm\sqrt{a}\)があるということは主張してきましたが、それと\(\pm\sqrt{a}\)しかないという主張とはまったく異なる主張であることを意識する必要があります。なぜなら、\(\pm\sqrt{a}\)の他に平方根があるならば、前者の「平方根として\(\pm\sqrt{a}\)がある」という主張はやはり正しいですが、後者の「平方根には\(\pm\sqrt{a}\)しかない」という主張は間違いになるからです。つまり、後者の主張を証明するためには、前者の主張に加えて「他に平方根がない」ことも証明しなければなりません。
「他に平方根がない」ことの証明は、最後にまとめて行いたいと思いますので、一先ず次は、実数\(a\)が負の数の場合について考えたいと思います。
実数\(a\)が負の数の場合について、実数\(a\)が負の数なので、\(a=-a’\)と置き直せば\(a’\)は正の実数です。したがって、実数\(a’\)には上述の議論より平方根が少なくとも二つあって\(\pm\sqrt{a’}\)と書き表すことができます。これと虚数\(i\)が\(-1=i^2\)であることから、\(a=-a’=(\pm\sqrt{a’}i)^2\)が成り立ちます。つまり、\(\pm\sqrt{a’}i\)を二乗すると\(a\)になるので、少なくとも\(\pm\sqrt{a’}i\)は\(a\)の平方根であることが分かりました。
実数\(a\)が\(0\)の場合については、少なくとも\(0\)が平方根になることは分かります。
他に平方根がないこと
それでは、最後に「他に平方根がない」ことを証明したいと思います。定義を振り返ると\(a = x^2\)を満たす、すべての数が平方根でした。式を変形すると、\(0 = x^2 – a\)であり、ここで\(a \geq 0\)でのみ定義されていた記号\(\sqrt{a}\)を拡張して、\(a\)が負の場合にも使えるように\(a < 0\)の場合には\(\sqrt{a}=\sqrt{-a}i(=\sqrt{a’}i)\)であるとすると、
\[0 = x^2 – a \Leftrightarrow 0 = (x+\sqrt{a})(x-\sqrt{a})\]
と因数分解することができます。\(a\)が正の数、\(0\)、負の数、どの場合でも上式の因数分解が成立していることを確認してみて下さい。ここで、\(x\)が複素数以外となる場合まで考えるとなると話が変わりますが、\(x\)が複素数であることを前提とすると、\(x\)が複素数であれば\(\sqrt{a}\)や\(-\sqrt{a}\)との和もやはり複素数となるので、\((x+\sqrt{a})\)と\((x-\sqrt{a})\)は共に複素数になります。
そうすると、複素数の積が\(0\)ならばいずれかは\(0\)であるという前述の命題より、\((x+\sqrt{a})\)または\((x-\sqrt{a})\)が\(0\)でなければなりません。ここで仮に、\(x\)が\(\sqrt{a}\)でも\(-\sqrt{a}\)でもなければ、このどちらも\(0\)にはならず矛盾してしまいます。したがって、その否定の\(x\)は\(\sqrt{a}\)または\(-\sqrt{a}\)であることが成り立ち、つまり、\(a\)の平方根\(x\)は、\(\sqrt{a}\)または\(-\sqrt{a}\)のどちらかである必要があり、「他に平方根がない」ことが証明できました。以上の議論が\(a\)が正の数、\(0\)、負の数、どの場合でも成立していることを確認してみて下さい。
以上より、実数\(a\)の平方根は、\(\pm\sqrt{a}\)の二つだけであることが分かりました。正確には、重根の場合には一つのこともあります。
ちなみに、複素数では「積が\(0\)ならばいずれかは\(0\)である」という命題が成り立ちますが、一般に積が成り立つ対象でこの命題が成立するとは限りません。例えば、過去に高校数学でも教えられていた行列では、この命題が成立するとは限らず、\(0\)ではない行列同士の積で\(0\)になってしまう例があります。そうなってくると、仮の話ですが、たとえ\(0 = (x+\sqrt{a})(x-\sqrt{a})\)のように因数分解できたとしても、\(\sqrt{a}\)でも\(-\sqrt{a}\)でもない解によって式が成立する場合がありえてしまい、必ずしも平方根が\(\pm\sqrt{a}\)の二つだけに限られない、、という結論もあり得てしまうわけです。
少し発展的な内容になりますが、この命題は、「複素係数(したがって実数係数も)の\(n \geq 1\) 次方程式は複素根を重複を含めて丁度\(n\)個持つ」という形式の代数学の基本定理の前提にもなっていることが分かります。つまり、一般の\(n\)次式の場合にも類似の議論を行うことができるということです(参考:恒等式の次数と係数、根の個数の条件の証明:発展:線形代数や代数学の基本定理との関連)。この命題の重要性が理解できると思います。
根号の乗法と除法における注意点
教科書にも記載されていますが、根号\(\sqrt{\ }\)を用いた計算は少し注意が必要です。まず、復習すると\(a > 0\)の場合には、\(\sqrt{a}\)は\(a\)の正の平方根を表し、それを拡張して\(a < 0\)の場合には、\(\sqrt{a} = \sqrt{-a}i \)と定義したのでした。後者は、言い換えて\(a=-a’\)とすると、\(\sqrt{a} = \sqrt{a’}i \)とも表されます。
そうすると、根号の中が掛け算\(a \cdot b\)や割り算(分数)\(\frac{a}{b}\)になっているときに、共に正の数\(a,b > 0\)であれば、
\[\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\]
\[\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\]
と根号を展開できるのです。なぜなら、右辺を二乗してみれば\(a \cdot b\)や\(\frac{a}{b}\)になり、その平方根であり、かつ、掛け算の結果も割り算の結果も正なので、その正の平方根であることが言えるからです。
しかしながら、掛け算\(a \cdot b\)については、どちらも負の数\(a,b < 0\)のとき、
\[\sqrt{a} \cdot \sqrt{b} = \sqrt{-a}i \cdot \sqrt{-b}i = -\sqrt{-a}\cdot\sqrt{-b} = -\sqrt{(-a) \cdot (-b)} = -\sqrt{a \cdot b}\]
であり、\(\sqrt{a} \cdot \sqrt{b}\)は\(-\sqrt{a \cdot b}\)となります。したがって、負の数\(a,b < 0\)のとき、\(\sqrt{a \cdot b} \neq \sqrt{a} \cdot \sqrt{b} = -\sqrt{a \cdot b}\)なので、平方根の積は展開できません。より詳しく言うと、\(\sqrt{a \cdot b}\)は\(a\)と\(b\)の負が相殺して実数の正の平方根\(\sqrt{a \cdot b}\)になっており、\(-\sqrt{a \cdot b}\)は実数の負の平方根になっています。
残りの\(a,b\)のどちらか一方が正でもう一方が負の場合には、虚数の平方根として等式が成り立つので展開できます。練習問題として確認してみて下さい。
また、割り算(分数)\(\frac{a}{b}\)については、分子\(a\)が正\(a > 0\)、分母\(b\)が負\(b < 0\)のとき、
\[\sqrt{\frac{a}{b}} = \sqrt{-\frac{a}{b}}\cdot i\]
であり、
\[\frac{\sqrt{a}}{\sqrt{b}} = \frac{\sqrt{a}}{\sqrt{-b}\cdot i} = -\frac{\sqrt{a}}{\sqrt{-b}}\cdot i = -\sqrt{-\frac{a}{b}}\cdot i\]
なので、したがって正負が逆なことから、
\[\sqrt{\frac{a}{b}} \neq \frac{\sqrt{a}}{\sqrt{b}}\]
となり、やはり、このときは平方根の割り算を展開することはできません。
残りの\(a < 0,\ b > 0\)や\(a < 0,\ b < 0\)の場合には、割り算を展開することができます。練習問題として確認してみて下さい。
以上をまとめると、掛け算の根号は\(a,b < 0\)のとき以外はそのまま展開することができ、割り算の根号は\(a > 0,\ b < 0\)のとき以外はそのまま展開することができます。結果を暗記するのではなく、定義を理解して計算すれば間違えないと思います。
おまけ:教科書の各章冒頭コラムについて
本サイトで参考にしている高校数学の教科書では、各章の始まりのページにその章で学ぶ内容の数学史的な位置付けを解説するコラムが掲載されています。どのコラムも短い中に洗練された内容が詰め込まれていて、生徒の各章を学ぶ意欲を喚起するには十分と感心されられるものになっています。このコラムを読めば、次にどのような勉強が必要で、どのような分野に応用があるのかまでを指し示してくれます。
ただ、高校生が一読でその意味を理解したり、その内容を学ぶための文献を見つけられるかは、とても難しいことです。もちろん、適切に解説をなされる先生と出会える機会があれば幸運ですが、どんな先生方にも得意分野というものがあります。同じ質問をしても答えは様々に異なるものです。複数の先生に質問をする、図書館に行く、ウェブを検索する、そして探し当てた解説を理解するために努力することが大切だと思います。
ここでは、特に数学Ⅱの第2章「複素数と方程式」で解説されている内容に少し発展として触れて、このページを終わりにしたいと思います。(第3章「図形と方程式」のデカルトについてのコラムも非常に重要な学問上の転機なのですが、以下、長くなり過ぎてしまったので割愛します。合理的に物事を考える方法:4.デカルトを参考にして下さい。)
まず、数学Ⅱの第2章「複素数と方程式」のコラム冒頭は、「驚くべきことに、2次方程式の解法は古代バビロニアの時代に知られていたらしい。」と始まります。この驚くべきことに、を高校生が実感できるかです。そのためには、古代バビロニアの時代を知らないといけません。私も詳しくは知りません、しかし、それがピタゴラスの時代をはるかに超え旧約聖書の時代のバベルの塔やメソポタミア文明が栄えた頃、「目には目を」のあのハンムラビ法典が倫理として厳然と存在する遠く古代文明の起こりのような、そんな時代にすら2次方程式の解法はあったと言うのです。
続く、未知数を記号で表す代数学が、インドで始まり、アラビア、ルネサンスのイタリア、ヨーロッパへと広がったという記述を読んで、いかに数学という知識がゆっくりと紆余曲折を経て伝わっていくのかということを実感できると共に、では、古代バビロニアの時代の2次方程式の解法は、代数を用いずにどうやって表現していたのかという疑問も浮かぶはずです。
そして、舞台は近世ヨーロッパに移り、\(n\)方程式の解法の話題がクローズアップされていきます。3次、4次までは解法が具体的に示され、「ガウス(1777-1855)は、高次の方程式も複素数の中に必ず解を持つこと、すなわち『代数学の基本定理』と呼ばれる結果を証明した。この結果は方程式の係数から解を具体的に求める方法を与えていない。」と続きます。つまり、解はある、けれど、具体的に求められるかは分からない。という状態があるのだということが高校生にとっては恐らく新鮮な驚きではないでしょうか。
このような物事の繊細な捉え方は、前述の章「『ある』『ない』『対応(どうある)』『表す』とは」でも解説しましたが、この世の中には往々にしてあり、とても良い思考訓練になります。例えば、あるのに書けない、あるのに表せない、あるのにどれくらいあるかは分からない、あるかないかはどちらかだが確率的にしか認識できない、あるかないかはどちらかだが絶対的な証明はできないなどなどです。このような難題に対して人類は、多大な労力を掛けて数学理論、科学理論、法理論等を構築してきた側面があります。
実際に、近世ヨーロッパでは5次以上の方程式の複素数解があるのだからその解法もあるだろうと、つまり、係数から加減乗除とべき根を取る操作により解を求める一般的な方法もあるだろうと考える数学者も多かっただろうと思いますが、その期待は新進気鋭の若き数学者アーベルとガロア(当時はただの抜群に数学ができる高校生か大学生)によって否定されます。つまり、二人は5次の方程式の係数から加減乗除とべき根を取る操作により解を求める一般的な方法は存在しないことを証明しました。特に、ガロアはコラムから引用すると「一般の次数の方程式に対し、解を係数を使って具体的に表す問題の本質を見抜いて解決し、群や体といった今日の代数学の対象となる基本概念を作った。」のです。
ここで触れておきたいのは、そもそも高校生にとっては、複素数以外に数はないの?とか、複素数以外だったら解が存在して具体的にも表せる数はないの?とか、どんな表し方でも表現できないの?とか、根源的な疑問がたくさん浮かんでくると思います。このような初めての概念に出会ったときに初めて浮かんでくる疑問というのは、その人が一生で一度だけ与えられる貴重な機会(初見の想像力が豊かに働く機会)とも言えるかと思います。その疑問のあるものは解決されていて、あるものは数学者たちを未だに悩ませているものもあるだろうと思います。だから、そのような疑問はまず大切に記録して、一つ一つ調べゆっくりと考え解決していくことをお勧めしたいです。
その上で、ガロアの引用に戻ると、かなりの重要情報が詰め込まれています。ガロアは「本質を見抜いて解決」し、その本質は「群や体」と呼ばれ、「今日の代数学の対象となる基本概念」になっているというのです。つまり、ガロアは単に5次以上の方程式の解法が存在しないことを証明しただけではなく、今日の代数学の基礎を発見したというわけです。今日の代数学というのは、つまり、この高校数学の教科書の先の大学で学ぶ代数学ということです。
ただ、大学での数学だからといってあまり難しく感じる必要はありません。小学校で学んだ算数が中学校で数学になり、古代バビロニアから古代ギリシャくらいの飛躍を遂げ、中学校で古代ギリシャから近世ヨーロッパの入り口へ、高校生で近世ヨーロッパの数学に入り込み、というようにこれまでも時代を順々に進んできており、その歩みがこの先も大学において近代・現代の数学へと進んで行くと捉えれば、今まで通り、一歩一歩進んでいくことになります。つまり、小学生が二次方程式の解法を知らないように、高校生が群や体を知らないだけであり、何で先に教えてくれなかったの?と思うくらいであれば先に進めば良いと思います。
その際には、焦って群や体をいきなり学ぼうとするよりは、一般的には初等整数論、集合論、線形代数学、微分積分学などを一通り学んでしっかりと考える力を付けてから取り組むと良いとも思います。「5次以上の方程式の係数から加減乗除とべき根を取る操作により解を求める一般的な方法は存在しないこと」を群や体の理論として学ぶのは、一般の大学数学科であれば3・4年生辺りになると思います。けれど、群や体とは何だろうという疑問に対しては、より平易に解説を試みた入門書が図書館にたくさんあると思いますので、まずそれらを手に取ってみるのも良いと思います。また、これだけインターネットが発達した現代では、大学数学のカリキュラムから解説、映像授業まで上手に検索をたどれば十分な情報を手に入れられます。
著者:L&M個別オンライン教室 瀬端隼也
公開日:2021年1月15日
修正日:2021年5月31日 第4章『おまけ:教科書の各章冒頭コラムについて』の第8段落「係数から具体的に求める一般的な方法」⇒「係数から加減乗除とべき根を取る操作により解を求める一般的な方法」
第4章『おまけ:教科書の各章冒頭コラムについて』の最終段落「係数から具体的に解を求める一般的な方法」⇒「係数から加減乗除とべき根を取る操作により解を求める一般的な方法」



※このサイトはreCAPTCHAによって保護されています。そのためGoogleのPrivacy PolicyとTerms of Serviceが適用されます。