対偶の証明について

【目次】
１．集合の包含関係を用いた証明
１－１．命題の推論関係と集合の包含関係が一致
１－２．補集合と包含関係の逆転
２．集合の包含関係を用いない証明
２－１．その他の証明方法
２－１－１．真理値を使った証明
２－１－２．ベン図を用いない証明

「集合と命題について」で説明した通り、集合と命題は切り離して考えられます。教科書（数研出版、高校数学の教科書、以下同じ。詳しくは、高校数学マスター基本方針：参考にする教科書を参照ください）では、「真な命題の対偶もまた真である」、つまり、任意の命題pと命題qについて、
\[(p \Rightarrow q)\hspace{5pt}\Leftrightarrow\hspace{5pt}(\lnot q \Rightarrow \lnot p) \tag{1}\]が成り立つことを、命題p,qで定まる集合の包含関係を用いて証明しています。（記号\(\lnot p\ \)と\(\ \overline{p}\ \)は同じ意味で、共に命題\(p\)の否定を表します。）

しかし、そのような集合の包含関係を持ち出さなくとも、\((1)\)は命題と推論のみで証明することができることをこのページでは説明します。教科書とは異なる考え方にも触れることで、集合と命題の関係、命題を使った論理についての少し深い理解が得られるようにしたいと思います。

集合の包含関係を用いた証明

まずは、一般に教科書で示される集合の包含関係を用いた証明を復習しましょう。

命題の推論関係と集合の包含関係が一致

第一に、命題の推論関係と集合の包含関係が一致するのでした。つまり、全体集合がUの変数xを含む任意の命題pと命題qについて、命題pと命題qが真である場合に、変数xが取りえる要素をそれぞれ集合Pと集合Qとすると、\[P\ =\ \{\ x\ |\ p(x)が真となる\ \} \\[10pt] Q\ =\ \{\ x\ |\ q(x)が真となる\ \}\]と集合Pと集合Qは書け、ただし、\(p(x)\)は変数xを含む命題pという意味です。\[(p \Rightarrow q)\hspace{5pt}\Leftrightarrow\hspace{5pt}P \subset Q \tag{2}\]が成立します。

ベン図を書くと、以下のようになります。

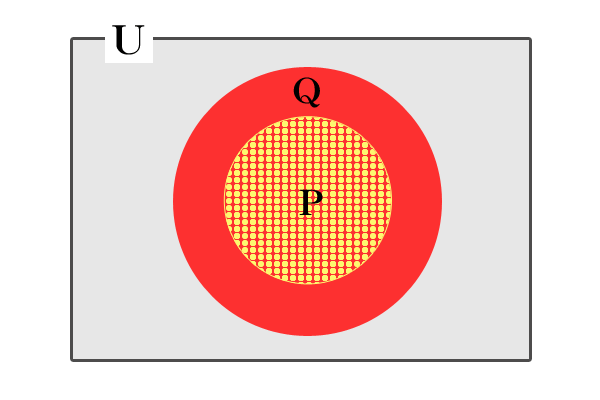
補集合と包含関係の逆転

見方を変えて、集合Pと集合Qのそれぞれの補集合に注目すると、以下のように包含関係が逆転していることが分かります。

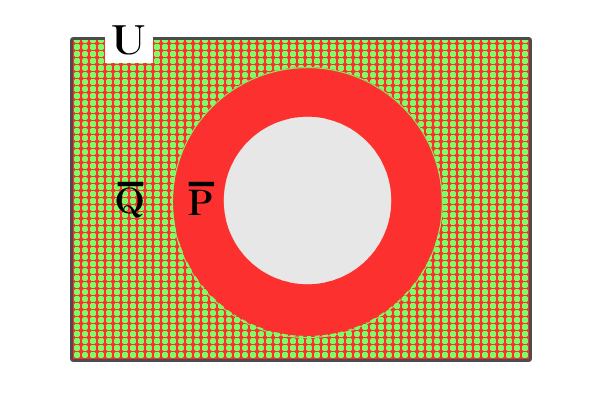
つまり、\(\overline{Q} \subset \overline{P}\)であることが分かり、ここから、
\[\overline{Q} \subset \overline{P}\hspace{5pt}\Leftrightarrow\hspace{5pt}P \subset Q \tag{3}\]が成り立ちます。

\((2)\)と同様に、\[(\lnot q \Rightarrow \lnot p)\hspace{5pt}\Leftrightarrow\hspace{5pt}\overline{Q} \subset \overline{P} \tag{4}\]であることも分かり、
結果、\((2)(3)(4)\)より、命題とその対偶の真偽が一致する\((1)\)が成り立つことが示せるのでした。

以上のような集合の包含関係を利用した証明は、命題が少なくとも一つの変数を含んで、その変数が取りえる対象の範囲を集合で定義できなければならないという制約を生じます。ちなみに、教科書にもある通り、そのような命題を構成する変数を含んだ文や式を条件と呼びます。

集合の包含関係を用いない証明

実際には、\((1)\)「命題とその対偶の真偽が一致する」を証明するのに集合は必要としません。したがって、変数を含まない一般の命題についても\((1)\)は成り立ち、応用範囲も広いということになります。

\[p \Rightarrow q \tag{5}\]が成り立つとき、その対偶\[\lnot q \Rightarrow \lnot p \tag{6}\]が成り立たないとすると、それは\(\lnot q\)が成り立たつときに\(\lnot p\)が必ず成り立つことがあってはいけないということを意味します。

一方で\(\lnot p \lor p\)は常に成り立つので\(\lnot p\)が必ず成り立つことがあってはいけないためには、\(\lnot q\)が成り立たつときに\(p\)が成り立つ場合が必要になるということです。

しかし、\(p\)が成り立つと\((5)\)より\(q\)が成り立ち、\(\lnot q\)が成り立つことと真偽が両立してしまう場合が必ずあるということになります。これは矛盾ですので、対偶\(\lnot q \Rightarrow \lnot p\)\((6)\)が成り立たなければなりません。

この証明には、矛盾と背理法を使っています。もし、「\((6)\)が成り立たないとすると、」や「\(q\)が成り立ち、\(\lnot q\)が成り立つことと真偽が両立してしまう場合が必ずあるということになります。これは矛盾ですので、対偶\(\lnot q \Rightarrow \lnot p\)\((6)\)が成り立たなければなりません」という部分がピンと来ない方は、この機会に矛盾と背理法について理解を深めると良いのではないかと思います。詳しくは、「矛盾と背理法について」をご覧ください。

その他の証明方法

その他にも色々と証明方法がありますが、ここでは二つの方法を説明します。発展的な学習となるので、ここでは用語の説明などはせずに基本的な方針だけを紹介しますので、興味を持った方は以下をヒントに学習を進めてみてください。

真理値を使った証明

各命題の真偽を場合分けし、すべての場合において真偽が一致すれば同値になります。

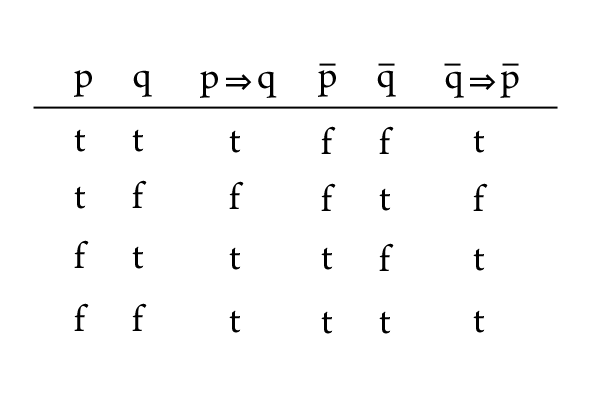
ベン図を用いない証明

集合を使っていても、ベン図を用いない証明も考えられます。つまり、\((3)\)の証明にベン図を用いないということです。

集合P、集合Qに対して、全体集合Uの要素は、
①\(P,Q\)に含まれる。
②\(P,\overline{Q}\)に含まれる。
③\(\overline{P},Q\)に含まれる。
④\(\overline{P},\overline{Q}\)に含まれる。
のいずれかの場合しかありません。

一方で、集合の包含関係は、
\[P \subset Q \\ P = Q \\ P \supset Q \]のみで、
\(P \subset Q\)の場合には、①③④の場合しかなく、
\(P = Q\)の場合には、①④の場合しかなく、
\(P \supset Q\)の場合には、①②④の場合しかありません。
つまり、集合Pと集合Qの包含関係は、全体集合Uの要素が①②③④のいずれに存在しうるかで定まります。
（ただし、記号\(\subset ,\supset\)は\(=\)を含まないこととします。）

ここで、集合Pと集合Qは一般の集合なので、\(\overline{Q} \subset \overline{P}\)について、\(\overline{Q}\)を集合\(P\)へ、\(\overline{P}\)を集合\(Q\)へ代入して考えてみると、

\(\overline{Q} \subset \overline{P}\)の場合には、全体集合Uの要素は、
\(\overline{Q},\overline{P}\)に含まれる。
\(\overline{\overline{Q}},\overline{P}\)に含まれる。
\(\overline{\overline{Q}},\overline{\overline{P}}\)に含まれる。
しかなく、計算するとこれは、①③④の場合と同じになります。

したがって、\(P \subset Q\)と同値になることが分かります。

公開日：２０１９年３月２９日
修正日：２０２３年１１月０３日
「２．集合の包含関係を用いない証明」が間違いではないのですが、分かりにくくよりよい証明を思いつきましたので書き直しました。
以下に、差し替え前の証明を残しておきます。ただし、「（←\(\lnot q\)が真であることが前提となります）」と「（\(\lnot q\)が真であることから）」を追記しました。この２点の前提を読み取るのはちょっと難しかったかと反省しています。

ちなみに、2023年11月1日付のコメントは以下の差し替え前の内容に対するものです。こちらも間違いではありませんが証明自体に対偶を用いている点はよろしくないかもしれません。

差し替え前：
【集合の包含関係を用いない証明】
実際には、\((1)\)「命題とその対偶の真偽が一致する」を証明するのに集合は必要としません。したがって、変数を含まない一般の命題についても\((1)\)は成り立ち、応用範囲も広いということになります。

\[p \Rightarrow q \tag{5-2}\]が成り立つとき、その対偶\[\lnot q \Rightarrow \lnot p \tag{6-2}\]が成り立たないとすると（←\(\lnot q\)が真であることが前提となります）、\[\lnot p \lor p\]は常に成り立つので（\(\lnot q\)が真であることから）、\[\lnot q \Rightarrow p \tag{7-2}\]が成り立たなければなりません。

すると、\((7-2)(5-2)\)より、\[\lnot q \Rightarrow q \tag{8-2}\]が成り立ちます（※１）。図に書くと、

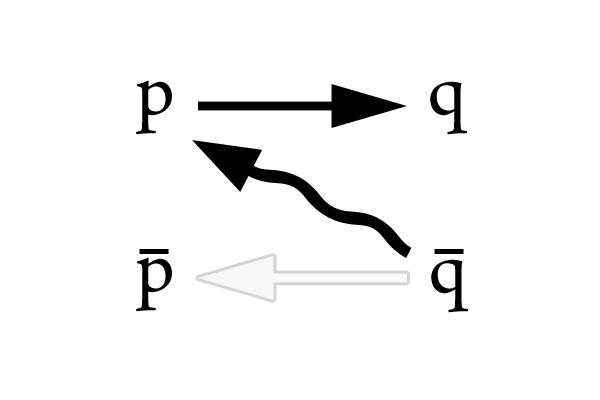
となります。

一般に命題\(p \Rightarrow q\)の真偽は、仮定\(p\)が真になる場合の結論\(q\)の真偽によって定まります。つまり、仮定\(p\)が真になる場合に、結論\(q\)が真になるのであれば命題\(p \Rightarrow q\)も真に、結論\(q\)が偽になるのであれば命題\(p \Rightarrow q\)も偽になります。

なぜなら、命題\(p \Rightarrow q\)は、仮定\(p\)が真になる場合の\(p\)と\(q\)の関係を定めているのであって、仮定\(p\)が偽になる場合の\(p\)と\(q\)の関係には何も言及していないからです。

そこで、\((8-2)\)においても仮定\(\lnot q\)が真になる場合を考えると、\((8-2)\)より\(q\)は真であり、そのためその否定の\(\lnot q\)は偽にもなり、矛盾します。したがって、\((6-2)\)が成り立ちます。

念のために言及すると、\(\lnot q\)が偽の場合にも\((6-2)\)は真になります。ここが命題の真理値などを学んでいない方には難しいかもしれませんが、数学では命題\(p\)が偽のとき、命題\(p \Rightarrow q\)は真となるからです。（疑問を感じた方は、数理論理学や数学基礎論の教科書を学んでみましょう。ただ、納得いく答えを見つけるには少し深堀する必要があると思います。）

したがって、どちらにせよ対偶\((6-2)\)が成り立ちます。

この証明には、矛盾と背理法を使っています。もし、「\((6-2)\)が成り立たないとすると、」や「\(\lnot q\)は偽にもなり、矛盾します。したがって、\((6-2)\)が成り立ちます。」という部分がピンと来ない方は、この機会に矛盾と背理法について理解を深めると良いのではないかと思います。詳しくは、「矛盾と背理法について」をご覧ください。

－ この注意は、大学の数学科の学生以上でなければ無理に理解しようとしなくても大丈夫です。 －
※１ \((8-2)\)は一見、矛盾しているようですが、矛盾とは言えません。\((8-2)\)は\(q\)が恒真文であることと同値になります。したがって、\(q\)が恒真文でないことを前提とすれば矛盾を生むことになります。そのため、\(q\)が恒真文であるか否かで場合分けしても良いと思います。
－ この注意は、大学の数学科の学生以上でなければ無理に理解しようとしなくても大丈夫です。 －