空間図形における二直線のなす角と二平面のなす角
【目次】
0.はじめに
1.空間図形における二直線のなす角
1-1.二直線のなす角の定義に必要な前提
1-2.二直線のなす角の定義
1-3.二直線のなす角の証明
1-3-1.証明の第一段階
1-3-2.証明の第二段階
1-3-3.証明の第三段階
2.二平面のなす角
2-1.二平面のなす角の定義と前提
2-2.二平面のなす角の一致と証明
3.付記:空間図形の勉強の仕方
はじめに
数学Aの教科書(数研出版、高校数学の教科書、以下同じ。詳しくは、高校数学マスター基本方針:参考にする教科書を参照ください)では、空間図形における二直線のなす角を一般に定義できると述べていますが、特に、二直線がねじれの位置にある場合について、二直線のなす角が定義できることの証明を省略しています。同様に、二平面のなす角も定義していますが、なぜそのような定義ができるのかという証明は省略しています。
このページでは、空間図形における二直線のなす角と二平面のなす角の定義を示すとともに、なぜそのような定義をすることができるのかをきちんと証明したいと思います。
空間図形における二直線のなす角
二直線のなす角の定義に必要な前提
それでは、まず、空間図形における二直線のなす角から見ていきましょう。
そもそも、空間において二直線の位置関係は、ねじれの位置、平行、一点で交わる、一致、の4つに分けられます。そのうちのねじれの位置は同一平面上にはなく、それ以外の平行、一点で交わる、一致は同一平面上にあります。(参照:空間における平行な直線の推移関係について:空間と平面における二直線の位置関係)
そして、二直線が同一平面上にある平行、一点で交わる、一致の場合には、二直線のなす角は空間図形であっても平面図形における定義を用いることができます。つまり、平行、一致の場合には角度を\(0^\circ\)とし、一点で交わる場合にはその一点の周りの鋭角について\(0^\circ\)より大きく\(90^\circ\)以下の角度として採用すれば良いわけです。そうすれば、角度\(0^\circ\)以上\(90^\circ\)以下の値が一つ定まったときに、二直線の相対的な位置関係を概ね表すことができるようになります。
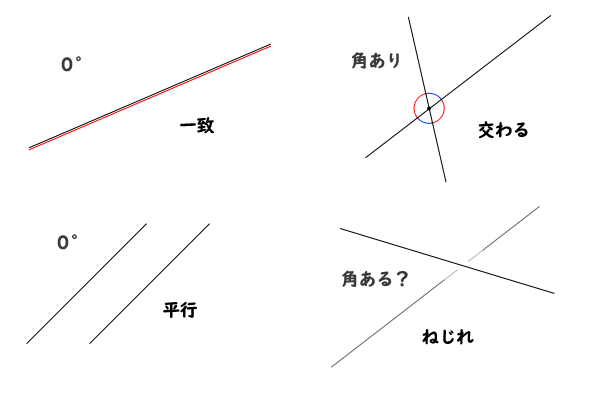
図1:空間図形における二直線のなす角
他方で、二直線が同一平面上にないねじれの位置にある場合には、交点がないので平面図形における定義をそのまま用いることはできません。そこで教科書で紹介されているように空間内のいずれかの一点を選び、その一点を二直線が通るように平行移動して、その平行移動した二直線に平面図形における角の定義を適用します。
もちろん、そのための前提には、どの一点に二直線を平行移動しても、その二直線の平面図形における角度が変わらないという事実が必要です。そうでなければ、平行移動する先の一点の取り方によって、二直線のなす角度が異なることになり、それはそれで異なる前提に基づいた考え方とするのであれば良いのですが、少なくとも二直線の位置関係によって一意に定まる数値ではなくなってしまいます。
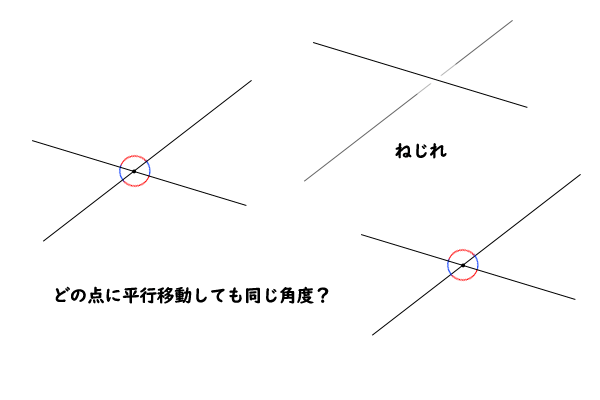
図2:ねじれの位置、どの点でも同じ角度?
二直線のなす角の定義
ここで実際の教科書の定義を引用すると、
2直線\(l,m\)が平行でないとき、任意の1点\(O\)を通る2直線\(l^{‘},m^{‘}\)を、それぞれ\(l,m\)に平行に引くと、\(l^{‘}\)と\(m^{‘}\)は1つの平面上にある。そして、\(l^{‘}\)と\(m^{‘}\)のなす2つの角は、点\(O\)のとり方によらず一定である。
この角を2直線\(l,m\)のなす角という。
とあります。
この教科書の記述は、前半の段落が命題、後半の一文が定義となっています。たしかに、前半の命題で点\(O\)のとり方によらず一定である、と指摘していますが、その証明がないわけです。
それでは次に、この教科書の前半の命題を【空間における二直線のなす角の一致】と名付けて証明を行いましょう。
二直線のなす角の証明
【証明】
この【空間における二直線のなす角の一致】の証明は、点\(O\)の取り方によって三段階に分けて行いたいと思います。正確にはその都度、明確にしますが、一通り先に提示すると、
第一段階は、点\(O\)が2直線\(l,m\)のいずれかの上にある場合です。
第二段階は、第一段階によって定められる平面\(\alpha\)に点\(O\)がある場合です。
第三段階は、平面\(\alpha\)に点\(O\)がない場合です。
以上の三段階のいずれにおいても、二直線のなす角が一致することを示します。
証明の第一段階
それでは、第一段階の証明から始めたいと思います。
2直線\(l,m\)のいずれかの上に点\(O\)がある場合ですが、どちらの場合を証明しても、もう片方の証明も同様に行えるので、ここでは直線\(m\)上に点\(O\)がある場合のみを証明します。
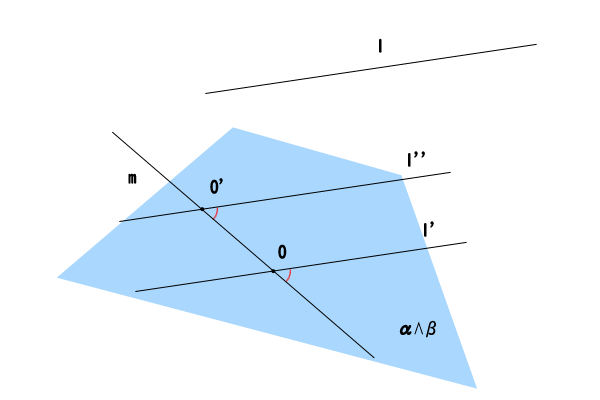
図3:第一段階、直線\(m\)上の点\(O\)
つまり、直線\(m\)上の点\(O\)を通る直線\(l^{‘}\)を直線\(l\)に平行になるように引きます。そうすると、二直線\(m,l^{‘}\)は交点\(O\)を持つので、二直線を含む平面がただ一つ決まります(参考:空間における平行な直線の推移関係について:前提命題:直線の決定と平面の決定)。この平面を平面\(\alpha\)としましょう。
次に、直線\(m\)上の点\(O\)と異なる点\(O^{‘}\)を取ります。そして、直線\(m\)上の点\(O^{‘}\)を通る直線\(l^{”}\)を直線\(l\)に平行になるように引きます。そうすると、空間における平行な直線の推移関係について:【命題:空間における平行な直線の推移関係】より、直線\(l\)に平行な直線\(l^{‘}\)と直線\(l\)に平行な直線\(l^{”}\)は、やはり平行なので、つまり、直線\(l^{‘}\)と直線\(l^{”}\)は平行になります。
空間において平行な二直線は同一平面上にあるので(参考:空間における平行な直線の推移関係について:平行線の定義の確認)、直線\(l^{‘}\)と直線\(l^{”}\)を含む平面を平面\(\beta\)とします。
ここで、平面\(\alpha\)は、直線\(l^{‘}\)と直線\(m\)上にある点\(O^{‘}\)を含み、
平面\(\beta\)も、直線\(l^{‘}\)と直線\(l^{”}\)上にある点\(O^{‘}\)を含んでいるので、
先ほど参考に示した【平面の決定】により、平面\(\alpha\)と平面\(\beta\)はただ一つに一致することが分かりました。
したがって、直線\(m,l^{‘},l^{”}\)は同一平面上にあります。点\(O\)の周りの直線\(m,l^{‘}\)のなす角と点\(O^{‘}\)の周りの直線\(m,l^{”}\)のなす角は、同一平面上の平行線のなす錯角であり、互いに等しいことが分かります。
したがって、直線\(m\)上のいずれに点\(O\)を取っても直線\(m,l^{‘}\)のなす角は等しいことが分かりました。これで第一段階の証明が終わりました。
証明の第二段階
それでは、次に第二段階の証明を行います。
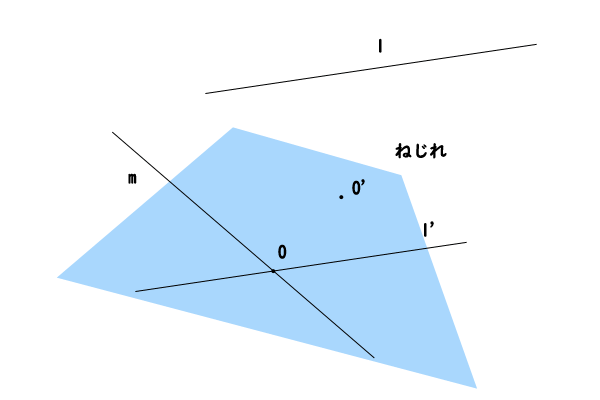
図4:第二段階、平面\(\alpha\)上の点\(O^{‘}\)
第一段階と同様に、直線\(m\)上のいずれかの点\(O\)を取り、点\(O\)を通る直線\(l^{‘}\)を直線\(l\)に平行になるように引きます。そして、二直線\(m,l^{‘}\)を含む平面を平面\(\alpha\)とします。
直線\(m\)上になく、平面\(\alpha\)に含まれる任意の点\(O^{‘}\)において、本命題【空間における二直線のなす角の一致】が成り立つことを示します。
平面\(\alpha\)において、点\(O^{‘}\)を通る直線\(m^{‘}\)を直線\(m\)に平行になるように引きます。
それではまず、点\(O^{‘}\)が直線\(l^{‘}\)にある場合を考えましょう。
そうすると、直線\(m\)と直線\(m^{‘}\)は平行なので、点\(O\)の周りの直線\(m,l^{‘}\)のなす角と点\(O^{‘}\)の周りの直線\(l^{‘},m^{‘}\)のなす角は、同一平面上の平行線のなす錯角であり、互いに等しいことが分かりました。
次に、点\(O^{‘}\)が直線\(l^{‘}\)にない場合を考えましょう。
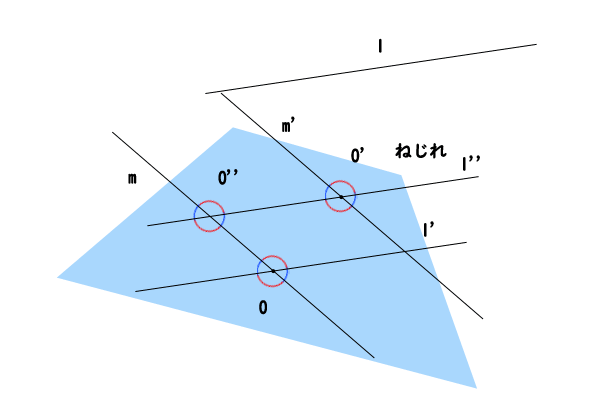
図5:第二段階、平面\(\alpha\)上の点\(O\)の直線\(l^{‘}\)にない場合の詳細
やはり、点\(O^{‘}\)を通る直線\(m^{‘}\)を直線\(m\)に平行になるように引きます。さらに、点\(O^{‘}\)を通る直線\(l^{”}\)を直線\(l\)に平行になるように引きます。
点\(O^{‘}\)が直線\(l^{‘}\)上にないので、直線\(l^{‘}\)と直線\(l^{”}\)は異なる直線になります。くわえて、直線\(l^{‘}\)と直線\(l^{”}\)は共に直線\(l\)に平行なので、先述の【命題:空間における平行な直線の推移関係】により、直線\(l^{‘}\)と直線\(l^{”}\)も平行になります。
直線\(m\)と直線\(l^{”}\)は平行でないので、その交点を点\(O^{”}\)とすると、直線\(l^{‘}\)と直線\(l^{”}\)は平行なので、点\(O\)と点\(O^{”}\)は異なる点で、同様に、直線\(m\)と直線\(m^{‘}\)も平行なので、点\(O^{‘}\)と点\(O^{”}\)は異なる点になります。
そうすると、直線\(l^{‘}\)と直線\(l^{”}\)は平行なので、点\(O\)の周りの直線\(m,l^{‘}\)のなす角と点\(O^{”}\)の周りの直線\(m,l^{”}\)のなす角は、同一平面上の平行線のなす錯角であり、互いに等しいことが分かります。
さらに、直線\(m\)と直線\(m^{‘}\)は平行なので、点\(O^{”}\)の周りの直線\(m,l^{”}\)のなす角と点\(O^{‘}\)の周りの直線\(m^{‘},l^{”}\)のなす角は、同一平面上の平行線のなす錯角であり、互いに等しいことが分かります。
したがって、この両者を合わせると、点\(O\)の周りの直線\(m,l^{‘}\)のなす角と点\(O^{‘}\)の周りの直線\(m^{‘},l^{”}\)のなす角が等しいことが分かりました。
したがって、直線\(m\)上になく平面\(\alpha\)に含まれるいずれの点\(O^{‘}\)を取っても直線\(m^{‘},l^{”}\)のなす角は等しいことが分かりました。これで第二段階の証明が終わりました。
証明の第三段階
それでは、次に第三段階の証明を行います。
第一段階と同様に、直線\(m\)上のいずれかの点\(O\)を取り、点\(O\)を通る直線\(l^{‘}\)を直線\(l\)に平行になるように引きます。そして、二直線\(m,l^{‘}\)を含む平面を平面\(\alpha\)とします。
平面\(\alpha\)上にない任意の点\(O^{‘}\)において、本命題【空間における二直線のなす角の一致】が成り立つことを示します。
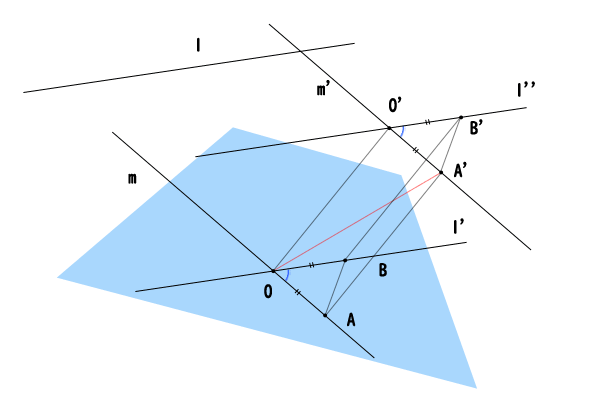
図6:第三段階、平面\(\alpha\)上にない点\(O\)の場合の詳細
第二段階と同様に、点\(O^{‘}\)を通る直線\(m^{‘}\)を直線\(m\)に平行になるように引き、点\(O^{‘}\)を通る直線\(l^{”}\)を直線\(l\)に平行になるように引きます。
直線\(m\)上に点\(O\)と異なる点\(A\)、直線\(l^{‘}\)上に点\(O\)と異なる点\(B\)を\(OA=OB\)となるように取ります。
ここで、点\(O^{‘}\)が平面\(\alpha\)上にないので、直線\(l^{‘}\)と直線\(l^{”}\)は異なる直線になります。くわえて、直線\(l^{‘}\)と直線\(l^{”}\)は共に直線\(l\)に平行なので、先述の【命題:空間における平行な直線の推移関係】により、直線\(l^{‘}\)と直線\(l^{”}\)も平行になります。
そこで、直線\(l^{”}\)上に\(OB\)と同じ方向に点\(O^{‘}\)と異なる点\(B^{‘}\)を\(OB=O^{‘}B^{‘}\)となるように取ります。
同様にして、直線\(m\)と直線\(m^{‘}\)は平行なので、直線\(m^{‘}\)上に\(OA\)と同じ方向に、点\(O^{‘}\)と異なる点\(A^{‘}\)を\(OA=O^{‘}A^{‘}\)となるように取ります。
今、直線\(m\)と直線\(m^{‘}\)は平行なので、この二直線を含む平面において、四角形\(OAA^{‘}O^{‘}\)を考えると、補助線\(OA^{‘}\)を引けば、平行線の錯角より\(\angle AOA^{‘}= \angle O^{‘}A^{‘}O\)が成り立ち、くわえて\(OA=OB\)、線分\(OA^{‘}\)を共有し、二角挟辺が等しいので、三角形\(OA^{‘}O^{‘}\)と三角形\(A^{‘}OA\)は合同と分かりました。
したがって、\(OO^{‘}=AA^{‘}\)であり、さらに、\(\angle O^{‘}OA^{‘} = \angle AA^{‘}O\)ということは、二直線\(OO^{‘},AA^{‘}\)の錯角が等しいので、二直線\(OO^{‘},AA^{‘}\)は平行であることも分かります。
四角形\(OBB^{‘}O^{‘}\)においても同様に考えると、\(OO^{‘}=BB^{‘}\)であり、二直線\(OO^{‘},BB^{‘}\)は平行であることが分かります。
したがって、\(AA^{‘}=BB^{‘}\)であり、【命題:空間における平行な直線の推移関係】により、二直線\(AA^{‘},BB^{‘}\)は平行であることが分かります。
したがって、四角形\(AA^{‘}B^{‘}B\)においても同様に考えると、\(AB=A^{‘}B^{‘}\)であり、二直線\(AB,A^{‘}B^{‘}\)は平行であることが分かります。
ここで、三角形\(OAB\)と三角形\(OA^{‘}B^{‘}\)について、\(OA=O^{‘}A^{‘}\)、\(OB=O^{‘}B^{‘}\)、\(AB=A^{‘}B^{‘}\)なので、二つの三角形は合同だと分かりました。
したがって、\(\angle AOB = \angle A^{‘}O^{‘}B^{‘}\)であり、点\(O\)の周りの直線\(m,l^{‘}\)のなす角と点\(O^{‘}\)の周りの直線\(m^{‘},l^{”}\)のなす角が等しいことが分かりました。
したがって、平面\(\alpha\)に含まれない任意の点\(O^{‘}\)を取っても直線\(m^{‘},l^{”}\)のなす角は等しいことが分かりました。これで第三段階の証明が終わりました。
以上で\(l^{‘}\)と\(m^{‘}\)のなす2つの角は、点\(O\)のとり方によらず一定であることが分かりました。□
二平面のなす角
二平面のなす角の定義と前提
教科書の二平面のなす角の定義を引用すると、
交わる2平面の交線上の点から、各平面上に、交線に垂直に引いた2直線のなす角を2平面のなす角という。
とあります。
ここで、この定義で省かれている前提は、交わる2平面の交線上の「任意の」点を取っても、各平面上に、交線に垂直に引いた2直線のなす角は等しいということです。そうでなければ、交わる2平面が定まったとしても、その2平面のなす角が一意に決まるわけではなく、それはそれで異なる前提に基づいた考え方とするのであれば良いのですが、この教科書の意図する定義とは異なります。
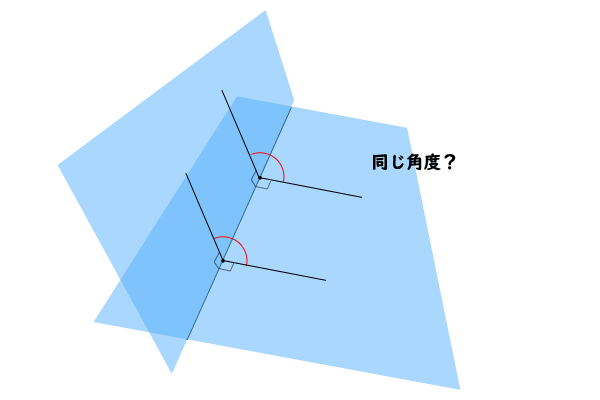
図7:二平面のなす角の前提
二平面のなす角の一致と証明
したがって、この定義の前提となる命題、
【命題:二平面のなす角の一致】
交わる2平面の交線上の任意の点から、各平面上に、交線に垂直に引いた2直線のなす角は等しい。
を証明したいと思います。
【証明】
それでは、二平面を\(\alpha,\beta\)、その交線を\(l\)、交線\(l\)上の任意の異なる2点を\(O,O^{‘}\)としましょう。
さらに、点\(O\)から平面\(\alpha\)上に、交線に垂直に引いた直線を\(m\)、
点\(O\)から平面\(\beta\)上に、交線に垂直に引いた直線を\(n\)、
点\(O^{‘}\)から平面\(\alpha\)上に、交線に垂直に引いた直線を\(m^{‘}\)、
点\(O^{‘}\)から平面\(\beta\)上に、交線に垂直に引いた直線を\(n^{‘}\)とします。
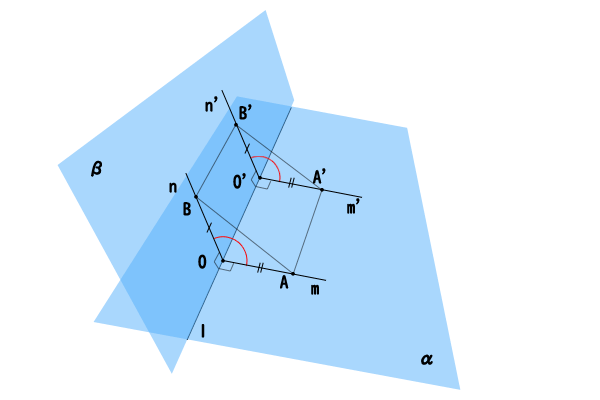
図8:二平面のなす角の一致の詳細
今、平面\(\alpha\)上において、直線\(l\)に対して、直線\(m\)と直線\(m^{‘}\)は共に垂直なので、二直線\(m,m^{‘}\)は平行であり、
同様に、平面\(\beta\)上において、二直線\(n,n^{‘}\)は平行であると分かります。
次に、平面\(\alpha\)において、直線\(m\)上に点\(O\)とは異なる点\(A\)を取ります。
二直線\(m,m^{‘}\)は平行なので、点\(A\)を取ったのと同じ方向に、直線\(m^{‘}\)上に点\(O^{‘}\)とは異なる点\(A^{‘}\)を、\(OA=O^{‘}A^{‘}\)となるように取ります。
同様にして、平面\(\beta\)において、直線\(m\)上に点\(O\)とは異なる点\(B\)を取ります。
二直線\(n,n^{‘}\)は平行なので、点\(B\)を取ったのと同じ方向に、直線\(n^{‘}\)上に点\(O^{‘}\)とは異なる点\(B^{‘}\)を、\(OB=O^{‘}B^{‘}\)となるように取ります。
ここで四角形\(OAA^{‘}O^{‘}\)について考えると、\(OA=O^{‘}A^{‘}\)であり、二直線\(m,m^{‘}\)は平行なので、【空間における二直線のなす角の一致】の3段階目で行った証明と同様にして、\(AA^{‘}=OO^{‘}\)であり、二直線\(AA^{‘},OO^{‘}\)が平行であることが分かりました。
同様にして、四角形\(OBB^{‘}O^{‘}\)について考えると、\(BB^{‘}=OO^{‘}\)であり、二直線\(BB^{‘},OO^{‘}\)が平行であることが分かります。
したがって、上記より\(AA^{‘}=OO^{‘}=BB^{‘}\)であり、二直線\(OO^{‘},AA^{‘}\)が平行かつ二直線\(OO^{‘},BB^{‘}\)が平行なので、【命題:空間における平行な直線の推移関係】より、二直線\(AA^{‘},BB^{‘}\)も平行であることが分かります。
そうすると、二直線\(AA^{‘},BB^{‘}\)が平行なので、4点\(A,A^{‘},B,B^{‘}\)は同一平面上にあり、四角形\(AA^{‘}B^{‘}B\)においても同様に考えて、\(AB=A^{‘}B^{‘}\)であり、二直線\(AB,A^{‘}B^{‘}\)が平行であることが分かります。
ここで、三角形\(AOB\)と三角形\(A^{‘}O^{‘}B^{‘}\)を考えると、\(AO=A^{‘}O^{‘}\)、\(BO=B^{‘}O^{‘}\)、\(AB=A^{‘}B^{‘}\)なので、三辺が等しく三角形\(AOB\)と三角形\(A^{‘}O^{‘}B^{‘}\)が合同であることが分かりました。
したがって、\(\angle AOB = \angle A^{‘}O^{‘}B^{‘}\)が成り立ちます。
以上より、交わる2平面の交線上の「任意の」点を取っても、各平面上に、交線に垂直に引いた2直線のなす角は等しいことが分かりました。□
付記:空間図形の勉強の仕方
最後に、ここまで我慢強く読んで頂けた方には理解をしていただけると思いますので、空間図形の勉強の仕方について一言言及すると、初めから空間図形を容易に想像できる人はかなり才能のある人で、そのような人はそれほど多くいません。そして、そのような才能のある方でも、漫然と想像を繰り返しているうちはどこかで乗り越えられない壁に突き当たります。
幾何学的な対象には多くの可能性があります。その複雑な現象を考えようとすればするほど、その様々な可能性の中から正解を導き出すために、前提にさかのぼり、前提からその正解を絞り込む論理的な思考過程が必要不可欠になります。この前提にさかのぼり、前提からその正解を絞り込むという、論理的な思考方法を身に付けられれば、自然と幾何学的な直観も豊かに正確なものに成長していくはずです。
そして、この論理的な思考方法は、幾何学の勉強で鍛えられる最も価値のある能力であり、その他の学問や仕事でも同様の役割を果たしてくれるだろうと思います。
著者:L&M個別オンライン教室 瀬端隼也
公開日:2019年12月9日
修正日:ー



※このサイトはreCAPTCHAによって保護されています。そのためGoogleのPrivacy PolicyとTerms of Serviceが適用されます。