直線と平面のなす角、その最小値性 ~論理と直観の解説と共に~
【目次】
0.はじめに
1.理数系科目が楽しくなる
2.論理と直観
2-1.本ページの試み、論理が直観を豊かにする
2-2.簡単に、論理とは何か
3.直線と平面のなす角
3-1.どのように定義するか
3-1-1.平面上の二直線の角度の定義
3-1-2.その他の角度の拡張定義
3-1-3.直線と平面のなす角の定義
3-2.最小値性の証明
3-3.試みの結果
はじめに
このページでは、空間において直線と平面のなす角をどのように定義すれば良いかを考えます。その中で、直線と平面のなす角として定義される角度が、直線と平面内の任意の直線のなす角の最小値であることが示唆されるので、その事実をきちんと証明して終わります。
くわえて、冒頭で論理と直観の違いやその関係性を簡単に解説し、このような幾何学的な考察を通して、論理的な考察が物事の直観や理解を育て養うということを体感して頂くことを目的とします。
理数系科目が楽しくなる
日本では高校で理数系科目が得意で、かつやる気を持って大学に入られた学生の中でも、一定数の学生が学問としての理数系科目の習得に挫折すると聞きます。その大きな原因は、大学(高校)の理数系科目で必要となる前提知識を日本の高校ではまったく教えられていないからです。
学問には、大きな流れがあり、ある知識にはその前提となる他の知識が必ずあります。その流れを掴めるか受容できるかどうかはその社会の持つ歴史、文化、宗教、政治等に依存し、個々人の感性にも大きく依存します。
効果の分かりやすいものは誰でも学ぼうとし、公教育のカリキュラムにも容易に取り入れることができます。しかし、残念ながら最終成果物に近い部類の知識だけを並べて学んでも、実際の理解や理解力が追い付いて行かないのです。
このページで解説する論理と直観というテーマは、数学のみならず学問においての古くて新しい重要な論題です。ここで紹介する論理に関する知識を理解できれば、高校と大学の理数系科目の習得がほぼ確実に楽になります。それ以上に、理解が容易になるので理数系科目を学ぶことが楽しくなり、理数系科目の教科書を気軽に手に取り、どんどん独学で先に進んで行けるようになるでしょう。
論理と直観
本ページの試み、論理が直観を豊かにする
前々回の付記:空間図形の勉強の仕方で、論理的な思考方法を身に付けられれば、自然と幾何学的な直観も豊かに成長していくと述べ、前回の余談:暗記と論証の違いで、理解力や考える力を付けるためには論証が大切であることを説明しました。
そこで今回は、論理的な考察が幾何の直観や理解を育て養うということを体感してもらう試みをしたいと思います。まず、この現段階で「直線と平面のなす角」という言葉から自分の思い描ける直観的な幾何学的事実をできる限り探究してみて下さい。そして、その事実を図や言葉で記憶するか書き留めてください。
このページでは、「直線と平面のなす角」についての論理的な考察を深めていきます。そして、その論理的な考察を読んだ後に、再び、自分が「直線と平面のなす角」という言葉からどれだけ幾何学的事実を直観的に思い描けるかを試してみて、現段階で得ていた図や言葉と比較してみてください。
このページを一歩一歩、読み進めてもらえれば、読了後の幾何学的な直観はより豊かになっているはずです。つまり、幾何学的なイメージをより正確に多角的に、あるいは、動的にも掴むことができているものと思います。
ただ、例えば、「直線と平面のなす角」が、直線と平面内の任意の直線のなす角の最小値である、ことが直観的に理解でき、すぐに証明まで思い描くような幾何学的な能力をすでに持っている方には、あまり効果はないかもしれません。
この実験のような試みは、単に幾何学における論理の重要性を体感してもらうためだけに行うのではなく、他の数学分野や学問、さらには、他の多くの実際的な物事においても、論理的な考察が物事の直観や理解を豊かにするということを体感してもらうための試みでもあります。
簡単に、論理とは何か
論理とは何かということについては、詳しく具体的な説明は論理とは何か、命題、集合と推論規則についてや合理的に物事を考える方法を読んで頂きたいと思います。ただ、ここでも簡単にだけ、論理とは何か、直観との違いやその関係性を説明したいと思います。
湯川秀樹博士は、「創造への飛躍」という著書でデカルトについて、「創造性という最もつかみにくい相手を把握しょうとしたこと自身がまた独創的であった。この意味においても彼は天才の中の天才であった。」と評しています。とても教養豊かな一流の科学者らしい捉え方です。
しかし、残念なのは科学者らしく、創造性に言及していながらソクラテスへの言及があまりなされていないことです。ソクラテスの産婆法(問答法)は、その名の通り、実際的な知恵を生み出す方法であり、ソクラテスもまた、「創造性という最もつかみにくい相手を把握しょうとした」天才の中の天才と言えるのです。
ソクラテスもデカルトも「真理や真実を見出すにはどうすれば良いか」という問いに向き合います。すると、どちらもまず「自他の考えを鵜呑みにしてはいけない」と思い当たります。疑問を持って考え、それでも正しいと思えなければ、それは真理や真実ではなかろうということです。
すると、疑問を持って考えるので、そこには疑問に答えるための根拠が必要になります。ソクラテスは、さらに、疑問を持ち続ければ、何も究極的な根拠として認められ得るものはなかろうと、無知の知という考えに至ります。デカルトは、「私は思うゆえに私はある」という命題だけは確実そうだ、というところで留まります。
もしも、ここでソクラテスやデカルトのように、論理とは何か、つまり、人が正しく考えるための方法とは何か、ということを疑問を持って考えると、何も絶対的に正しい方法や枠組みというのはないでしょう。
ただ、ソクラテスやデカルトが、ソクラテスの問答法やデカルトの探究方法を提案したように、人が正しく考えるためにそれなりに使える方法、枠組み、コツというものはありそうなのです。(ソクラテスの問答法、デカルトの探究方法の詳細については、上記の「合理的に物事を考える方法」ページを参照ください)
堂々巡りのようですが、まず第一にそれが疑問を持って考えるということであり、この疑問を持ち、根拠を得るということを逆にたどれば、ある根拠が正しいからこの主張が正しい、という推論になります。つまり、根拠を求めること、逆に、正しい推論を行うこと、これが論理の骨格になります。
さらに、様々な観点から色々な提言があります。簡単に済ませるために列挙に留めると、①疑問を持って根拠を求め、逆に、正しい推論を行う、②推論から矛盾を排除する、③推論の順序や重要度を意識する、④すべてを考えに含めて漏れを許さない、⑤分解して原理を見出し、原理から推論する、⑥対象と関係を明確にする、⑦分類に整理する、⑧概念の包含関係を意識する、などです。
以上のようなことに気を付けて考えることが、論理的に考えるということになります。そうすると、このような注意点を外れて、根拠を明確にせず、漠然とした経験や無意識の気付きによって思い描くことが、直観による考察と言えるかと思います。
このページでは、そのような直観による考察も、伝聞や曖昧な経験ではなく、論理的に考察する経験を積み重ねることで、「直観的な思い付きや理解」でさえも練磨できるということを示そう、というわけです。
それでは、ここで説明した「論理」を意識して、以降の解説をお読みください。一々、この箇所で①~⑧のいずれを用いましたという注意書きは煩雑になるので入れませんが、注意深く読み進めれば①~⑧のいずれもが幾つもの場面で用いられていることが分かると思います。
直線と平面のなす角
どのように定義するか
空間における直線と平面のなす角は、どのように定義すればよいでしょうか。一緒に考えてみたいと思います。
平面上の二直線の角度の定義
まず、そもそも基本的な角度という概念自体は、同一平面上の二直線について定義されました。同一平面上の二直線の位置関係は、①一致、②一点が交わる、③平行の3種類しかなく、その中の②一点が交わる場合において、角度は、一点が交わる二直線の位置関係をさらに区別し一意に表すための量として導入されます。その際に、①一致や③平行の場合を角度\(0^{\circ}\)とするかという論点もあります。
その他の角度の拡張定義
そして、その同一平面上の二直線についての角度の定義を基礎として、空間における二直線のなす角度や二平面のなす角度が拡張されて定義されるのでした(参照:空間図形における二直線のなす角と二平面のなす角)。
空間における二直線のなす角度は、空間内の任意の一点へ元の二直線と平行な二直線を引いて、その平行な二直線がなす角度を用いるのでした。この定義の前提には、空間内の任意の一点においてその平行な二直線がなす角度は等しいという事実がありました。
空間における二平面のなす角度は、二平面の交線上の任意の一点から各平面において引いた交線の二垂線がなす角度を用いるのでした。この定義の前提には、二平面の交線上の任意の一点においてその二垂線がなす角度は等しいという事実がありました。
つまり、どちらの場合にも同一平面上の二直線についての角度の定義を結局は用いています。その際に、どの同一平面上の二直線を用いるかについて、一意には定まらず選択肢が無限にあるのですが、結局は、それらすべての角度が等しいことを根拠として、定義の拡張に成功しています。結論として、角度という一意の量によって、空間における二直線や二平面の位置関係を表せているのです。
したがって、空間における直線と平面のなす角の定義についても、同一平面上の二直線の定義に帰着させること、その角度という一意の量によって、空間における直線と平面の位置関係がきちんと定まる必要があることが分かります。
直線と平面のなす角の定義
まず、空間における直線と平面の位置関係を整理すると、①平面に直線が含まれる、②一交点を持つ、③平行の3種類しかなく、同一平面上の二直線の角度と同様に、①平面に直線が含まれるや③平行の場合を角度\(0^{\circ}\)とするかという論点はありそうですが、それはとりあえず置いておいて、②一交点を持つ場合の角度の定義を考えましょう。
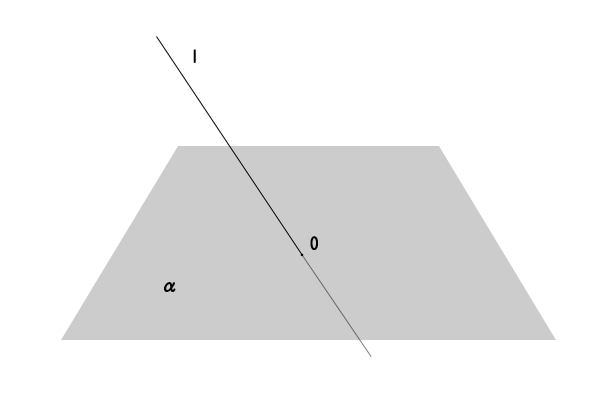
図1:直線と平面と交点
それでは、直線\(l\)が平面\(\alpha\)と交点\(O\)を持つとします。「同一平面上の二直線の定義に帰着させる」には、少なくとも直線が二つ必要になるわけですが、直線\(l\)はその一つとして明らかに選択する必要があるでしょう。そうすると、もう一つ直線を選ぶことになりますが、平面\(\alpha\)との角度なのですから、平面\(\alpha\)内のいずれか一つの直線を選ぶことになりそうです。
さらに、「同一平面上の二直線の定義に帰着させる」には、その字義通り、同一平面上に二直線がある必要があります。そうすると、平面\(\alpha\)内の直線で直線\(l\)と同一平面上にあるのは、交点\(O\)を通る直線のみだと分かります。他の平面\(\alpha\)内の直線は、直線\(l\)とねじれの位置にあります。
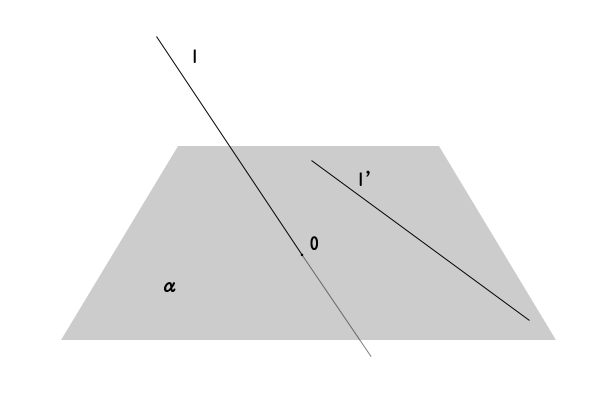
図2:直線と平面内の直線
【直線\(l\)と平面\(\alpha\)内の交点\(O\)を通らない直線が同一平面上にないことの証明】
念のため証明を付けておくと、なぜなら、仮に、平面\(\alpha\)内の交点\(O\)を通らない直線で直線\(l\)と同一平面上にある直線\(l^{‘}\)があったとすると、両者は同一平面上にあって交点がないので平行ということになります。ここで、直線\(l^{‘}\)に平行で交点\(O\)を通る直線を直線\(l^{”}\)とすると、直線\(l^{”}\)は平面\(\alpha\)内の直線です。一方で、直線\(l\)も直線\(l^{‘}\)に平行な交点\(O\)を通る直線であり、そのような直線は空間内において一つしかありません。したがって、直線\(l\)と直線\(l^{”}\)は同一の直線ですが、これは、直線\(l\)が平面\(\alpha\)内の直線であることになり矛盾します。
したがって、平面\(\alpha\)内のいずれか一つの直線を選ぶならば、交点\(O\)を通る直線を選べば良さそうなことが分かります。
このことは、空間における二直線のなす角の定義を振り返れることでも納得できます。空間における二直線のなす角は、二直線をどのように平行移動しても変わらないのでした。したがって、平面\(\alpha\)内の交点\(O\)を通らない直線を、交点\(O\)を通るように平行移動しても、直線\(l\)とのなす角度は変わりません。そのため、直線\(l\)と平面\(\alpha\)内のすべての直線とのなす角度を考える場合であっても、直線\(l\)と平面\(\alpha\)内の交点\(O\)を通る直線とのなす角度のみを考えさえすれば、十分であることが分かります。
それでは、平面\(\alpha\)内の交点\(O\)を通る直線の中に、直線\(l\)と平面\(\alpha\)の位置関係を決定づけるような、直線\(l\)との角度を持つ直線はありそうでしょうか。
その疑問に答えるためには、まず、平面\(\alpha\)内の交点\(O\)を通る直線と直線\(l\)との角度を具体的に考えてみましょう。
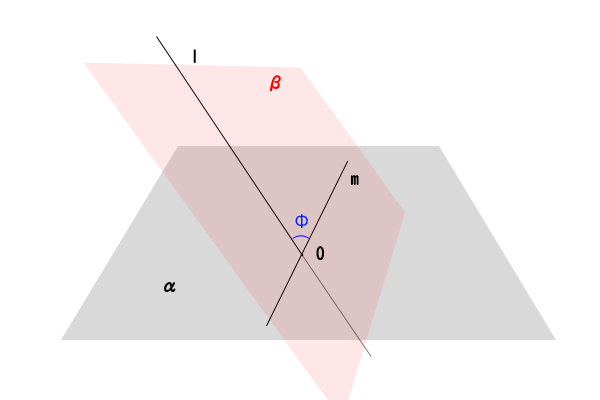
図3:直線と平面内の交点を通る直線のなす角度
平面\(\alpha\)内の交点\(O\)を通る任意の直線を直線\(m\)とします。直線\(l\)と直線\(m\)は交点\(O\)を持つので、同一平面上にあります(参考:空間における平行な直線の推移関係について:前提命題:直線の決定と平面の決定)。その同一平面を平面\(\beta\)とします。つまり、直線\(l\)と直線\(m\)の角度とは、平面\(\beta\)内の交点\(O\)周りに直線\(l\)と直線\(m\)によってできる角度ということになります。
ここで、この平面\(\beta\)内の直線\(l\)と直線\(m\)の角度を\( 0^{\circ} \le \phi \le 180^{\circ}\)としましょう。そうすると、直線\(m\)は点\(O\)を中心として平面\(\alpha\)内で一回転できるので、角度\(\phi\)は、直線\(m\)の取り方によって一定ではないことが分かります。
では、直線\(l\)と平面\(\alpha\)の位置関係を決定づけるような、直線\(l\)との角度\(\phi\)を持つ直線\(m\)はどこかにあるでしょうか。
それでは決定的な一打として、補助線を引いてみましょう。つまり、平面\(\alpha\)に対して点\(O\)を足とする垂線を下ろしてみます。この垂線を垂線\(h\)とすると、垂線\(h\)はただ一つのみあります。
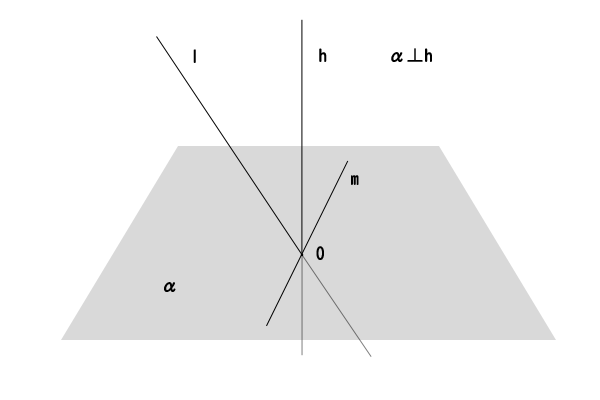
図4:平面と垂線
【平面\(\alpha\)に対して点\(O\)を足とする垂線\(h\)はただ一つあることの証明】
念のため証明を付けておくと、平面\(\alpha\)内で点\(O\)を通る直線\(m^{‘}\)を一つ取り、平面\(\alpha\)とその直線\(m^{‘}\)で交差する平面を平面\(\gamma\)とします。さらに、平面\(\alpha\)内で直線\(m^{‘}\)と点\(O\)で直交する直線\(m^{”}\)を引きます。そうすると、空間における二平面のなす角度の定義より、平面\(\alpha\)と直線\(m^{”}\)に垂直な平面\(\gamma\)が書けます。さらに、平面\(\gamma\)内において直線\(m^{‘}\)に点\(O\)において直交する直線を書けば、この直線は平面\(\alpha\)内の点\(O\)を通る二直線\(m^{‘},m^{”}\)に対して直交しています。したがって、この直線が垂線\(h\)となります(参照:平面に垂直な直線(平面に直交する直線、垂線)について)。仮に、垂線\(h\)が二つあったとすると、点\(O\)とその二垂線を含む同一平面が一つ定まります。その同一平面を平面\(\gamma^{‘}\)とし、平面\(\alpha\)と平面\(\gamma^{‘}\)の交線を直線\(m^{”’}\)とすると、二垂線は平面\(\gamma^{‘}\)内において点\(O\)を通る異なる二直線なので、直線\(m^{”’}\)とのなす角度も異なるはずです。しかし、同時に平面\(\alpha\)の二垂線なので、どちらも直線\(m^{”’}\)と直交していて角度は等しくなければならず、矛盾します。
垂線\(h\)をただ一つ引けると、直線\(l\)と垂線\(h\)は点\(O\)を通る二直線なので、同一平面上にあります。空間における二平面の位置関係は、①一致する、②一直線で交差する、③平行の3種類しかないので、今、この同一平面と平面\(\alpha\)は点\(O\)を共有していて、一致はしていないので、②一直線で交差するしかありません。すると、その交差する直線は点\(O\)を通るので、先ほどから考えていた、ある直線\(m\)の一つであることが分かります。そうすると、直線\(l\)と垂線\(h\)を含む同一平面は、直線\(l\)と直線\(m\)を含む平面\(\beta\)の一つでもあることが分かります。
それでは、再び先ほどの疑問に戻って、この垂線\(h\)によって定まるこの直線\(m\)が、直線\(l\)と平面\(\alpha\)の位置関係を決定づけるような、直線\(l\)との角度\(\phi\)を持つ直線\(m\)と言えるでしょうか。
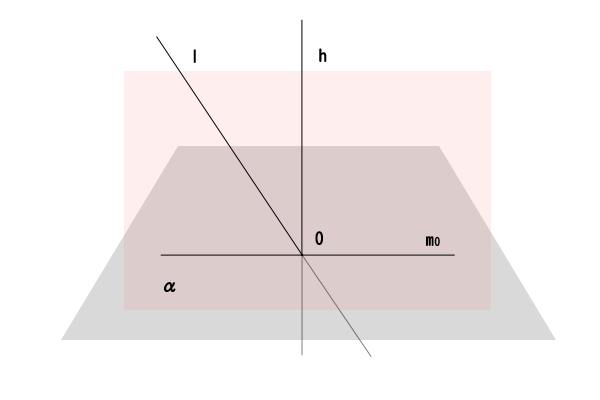
図5:垂線によって定まる点\(O\)を通る特別な直線
答えはイエスです。平面\(\alpha\)に対して、点\(O\)を通る垂線\(h\)は一つに定まるので、この特別な直線\(m\)を直線\(m_{0}\)とすると、直線\(m_{0}\)は直線\(l\)と平面\(\alpha\)の位置関係のみによって、どのような場合であっても一つに定まることが分かります。そして、その角度\(\phi\)を指定しさえすれば、直線\(l\)が平面\(\alpha\)に対してどのくらい倒れた位置関係にあるのかが、角度という一意の量によって表すことができます。
他方で、その他の点\(O\)を通る任意の直線\(m\)は、垂線\(h\)から定まるこの特別な直線\(m_{0}\)を基準としなければ、その位置を指定することができません。したがって、たとえその角度\(\phi\)を指定したとしても、直線\(l\)と平面\(\alpha\)の位置関係をその角度\(\phi\)によって指定することはできません。
したがって、たしかに、このように直線\(m_{0}\)を用いて、空間における直線と平面のなす角を定義すれば、直線\(l\)が平面\(\alpha\)に対してどのくらい倒れた位置関係にあるのかが、角度という一意の量によって表すことができることが分かりました。
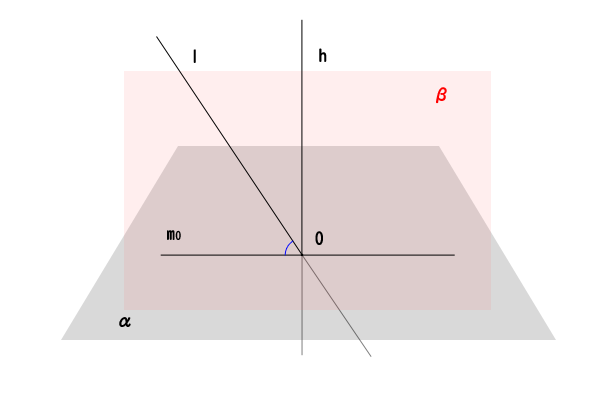
図6:直線と平面のなす角の定義
きちんと定義を明記すると、
直線\(l\)が平面\(\alpha\)と交点\(O\)を持つとき、点\(O\)を足とする平面\(\alpha\)の垂線\(h\)と直線\(l\)を含む平面\(\beta\)について、平面\(\alpha\)と平面\(\beta\)の交わる直線\(m_{0}\)と直線\(l\)のなす角を、直線\(l\)と平面\(\alpha\)のなす角という。
となります。
くわえて、ここで平面\(\alpha\)において直線\(m_{0}\)と点\(O\)を通る任意の直線\(m\)がなす時計回りの角度を\(0^{\circ} \leq \theta \leq 180^{\circ}\)とすると、角度\(\theta\)が大きくなるほど、直線\(l\)と直線\(m\)がなす角度\(\phi\)も大きくなるようにみえます。
これこそ幾何的な直観の世界に半歩入っていると思いますが、このようなことを特別な訓練をせずとも日常の経験から正確にイメージできる人もいれば、できない人もいます。どちらにせよ、このページの目的は、このような直観的なイメージを論理的な考察の訓練で豊かにできるということを示すことであり、その訓練法の内容と成果を実感して頂くことにあります。
だから、ここでこの事実が直観的にピンと来ないとか、そんなこと普通は気付けないよ、という人にこそ、このページは最大の効果を発揮できると思います。とにかく、この事実については次の節で念入りに証明を行いますので、ここでは一旦、この事実が正しいとして考えます。
そうであるならば、直線\(m_{0}, \theta = 0^{\circ}\)のときに角度\(\phi\)は最小値を取ることになります。空間内の二直線のなす角度の定義より、直線の平行移動を考慮すれば、それはつまり、直線\(l\)と平面\(\alpha\)内の任意の直線のなす角の最小値が、直線\(l\)と直線\(m_{0}\)のなす角度ということになります。
直線\(l\)と平面\(\alpha\)内の任意の直線のなす角の最小値が、直線\(l\)と平面\(\alpha\)の位置関係を一意に決定するかというと、もちろん、この場合には一意に決定するのですが、色々と特殊な条件を考慮した場合には必然とも言えないかもしれません。ただ、少なくとも最小値は必ず一つしかありませんので、直線\(l\)と平面\(\alpha\)の位置関係を表す量として、それなりに有意義な定義であることも分かります。
最小値性の証明
それでは、直線\(l\)と平面\(\alpha\)内の任意の直線のなす角の最小値が、直線\(l\)と直線\(m_{0}\)のなす角度であることを示します。
すでに、空間内の二直線のなす角度の定義より、直線の平行移動を考慮すれば、直線\(l\)と平面\(\alpha\)内の任意の直線のなす角を考えるには、直線\(l\)と平面\(\alpha\)内の点\(O\)を通る直線のなす角を考えれば十分であることに言及しました。各図形の名称もここまでのところ名付けてきた通りに援用していきたいと思います。
まず、証明の本筋ではありませんが、幾何的な直観を豊かにするために、直線\(l\)と直線\(m\)を含む平面\(\beta\)の集合\(X\)と直線\(l\)を軸ととして回転する平面\(\beta^{‘}\)の集合\(Y\)が一致することを確認しましょう。
つまり、直線\(l\)と直線\(m\)を含む任意の平面\(\beta\)は、直線\(l\)を通っているので、直線\(l\)を軸ととして回転する平面でもあり、集合\(Y\)に属します。
一方で、直線\(l\)を軸ととして回転する平面\(\beta^{‘}\)は、直線\(l\)は平面\(\alpha\)と一点で交わっているので、平面\(\alpha\)と平面\(\beta^{‘}\)は一致もせず、平行でもないので、交線を持ちます。交点\(O\)は平面\(\alpha\)と直線\(l\)に含まれているので、平面\(\alpha\)と平面\(\beta^{‘}\)に含まれており、つまり、その交線に含まれています。そうすると、その交線は、平面\(\alpha\)内で点\(O\)を通る直線なので、先述の直線\(m\)であることも分かります。したがって、平面\(\beta^{‘}\)は、直線\(l\)にくわえて直線\(m\)を含んでいるので、集合\(X\)に属しています。
したがって、集合\(X\)と集合\(Y\)は、平面を要素とする集合として一致していることが分かります。そうすると、直観的なイメージとして、平面\(\alpha\)の点\(O\)の周りに直線\(m\)を一回転して生じる直線\(l\)と直線\(m\)を含む平面\(\beta\)の集合\(X\)と、直線\(l\)を軸として回転する平面\(\beta^{‘}\)の集合\(Y\)が、一致して同時に回転している幾何的なイメージが描けますでしょうか。
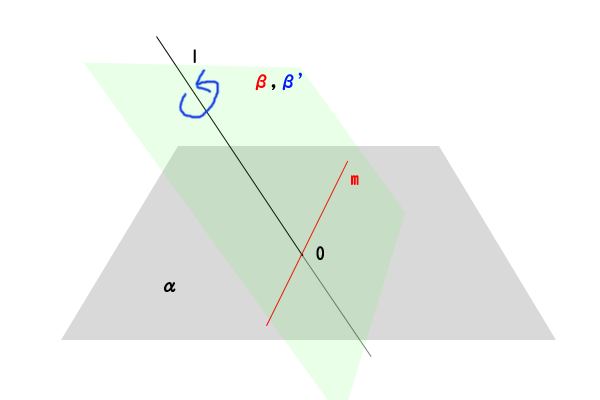
図7:直線\(l\)を含む平面\(\beta\)
これはつまり、同じ直線\(l\)を通る平面の集合\(X,Y\)を、直線\(m\)との関係で捉えるか、直線\(l\)を軸とする角度との関係で捉えるか、同じ対象を二つの異なる対象との関係で捉えていることに他なりません。このように、一つの対象を異なる関係で相対的、多面的に理解することが数学の基本であり、直観や理解に深みや豊かさを与えるポイントになります。
それは、結局、数学における理解とは、一つの数学的対象があったときに、他の数学的対象との関係を明らかにしていくことに他ならないからです。この例で言えば、直線\(l\)を通る平面の集合を理解するために、直線\(l\)との角度による位置の決定関係、別の直線\(m\)による位置の決定関係を明らかにしています。
それでは、少し直観的なイメージを豊かにしたところで、本題の証明に入っていきたいと思います。
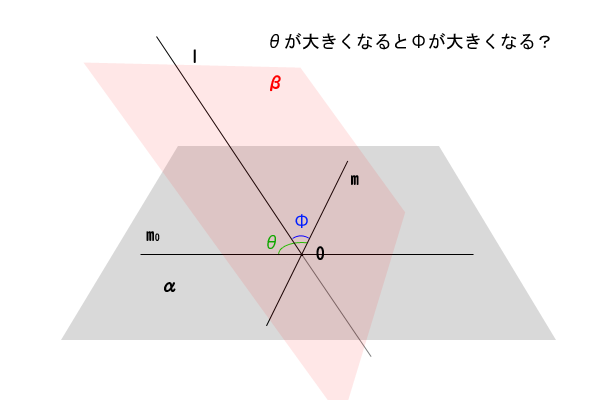
図8:\(\theta\)と\(\phi\)の大小関係
まず、直線\(l\)の点\(O\)と異なる点\(A\)を取ります。点\(A\)を通り垂線\(h\)に平行な直線が一つ引けますので、この直線を直線\(h^{‘}\)とします。垂線\(h\)と直線\(h^{‘}\)は平行なので、空間図形の平面の垂線の定義と二直線のなす角から、直線\(h^{‘}\)も平面\(\alpha\)の垂線であることが分かります。垂線\(h^{‘}\)の平面\(\alpha\)上の足を点\(H\)とします。
そうすると、先ほど、直線\(l\)と垂線\(h\)を含む平面と平面\(\alpha\)の交線を特別な直線\(m_{0}\)としましたが、この直線\(l\)と垂線\(h\)を含む平面を平面\(\beta_{0}\)とすると、垂線\(h^{‘}\)は直線\(l\)上の点\(A\)を通る垂線\(h\)に平行な直線なので、平面\(\beta_{0}\)に含まれています。したがって、垂線\(h^{‘}\)の足の点\(H\)は、平面\(\alpha\)との交線である直線\(m_{0}\)に含まれています。つまり、直線\(HO\)と直線\(m_{0}\)は一致していると分かります。
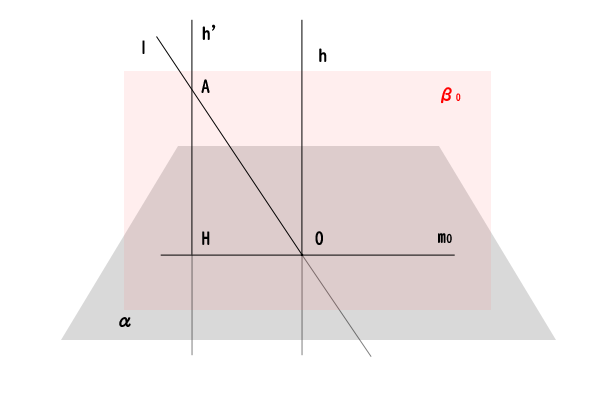
図9:垂線\(h^{‘}\)を引く
次に、線分\(HO\)を半径に点\(O\)を中心にして、補助円\(c\)を描きます。点\(O\)を通る任意の直線\(m\)と補助円\(c\)の時計回りの角度が\(0^{\circ} \leq \theta \leq 180^{\circ}\)になる側の交点を点\(B\)とします。同様にして、直線\(m\)と異なる点\(O\)を通る任意の直線\(m^{‘}\)を取り、角度\(0^{\circ} \leq \theta \leq 180^{\circ}\)と点\(B\)とは異なる、角度\(0^{\circ} \leq \theta^{‘} \leq 180^{\circ}\)と点\(B^{‘}\)を取ります。
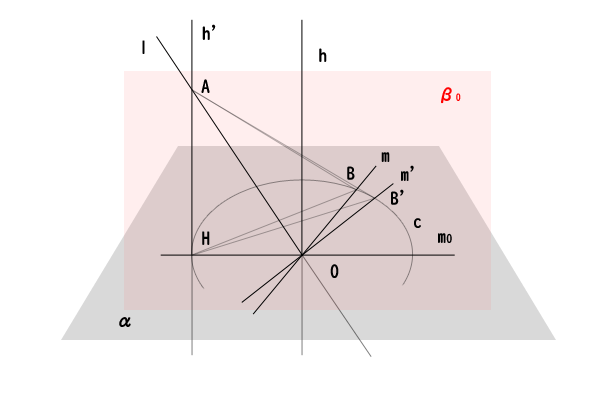
図10:補助円\(c\)を引く
そうすると、中心角と弧、弧と弦の大小関係から、
\[\theta\ \lt\ \theta^{‘}\ \Leftrightarrow\ \stackrel{\frown}{HB}\ \lt\ \stackrel{\frown}{HB^{‘}}\ \Leftrightarrow\ HB\ \lt\ HB^{‘}\]
が成り立ちます。
次に、三角形\(AHB\)と三角形\(AHB^{‘}\)を考えると、辺\(AH\)は平面\(\alpha\)の垂線\(h^{‘}\)なので\(\angle AHB = \angle AHB^{‘}=90^{\circ}\)で、共に辺\(AH\)を共通に持つ直角三角形であることが分かります。
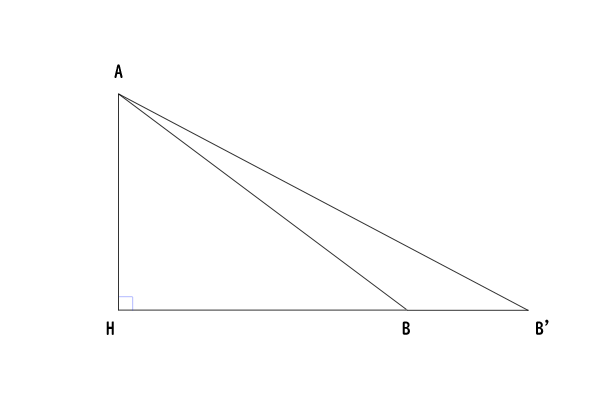
図11:二つの直角三角形
したがって、二つの直角三角形の辺\(HB\)と辺\(HB^{‘}\)を重ね合わせて考えた場合に、三角形\(ABB^{‘}\)について、\(\angle ABB^{‘}\)は鈍角であり、\(\angle AB^{‘}B\)は鋭角なので、三角形の辺の長さと角の大きさの関係より、\(AB \lt AB^{‘}\)が分かります。
まとめると、
\[HB\ \lt\ HB^{‘}\ \Rightarrow\ AB\ \lt\ AB^{‘}\]
が分かりました。
次に、直線\(l\)と直線\(m\)を含む平面\(\beta\)上について考えると、点\(O\)を中心として半径\(OB\)の補助円\(c^{‘}\)を書きます。
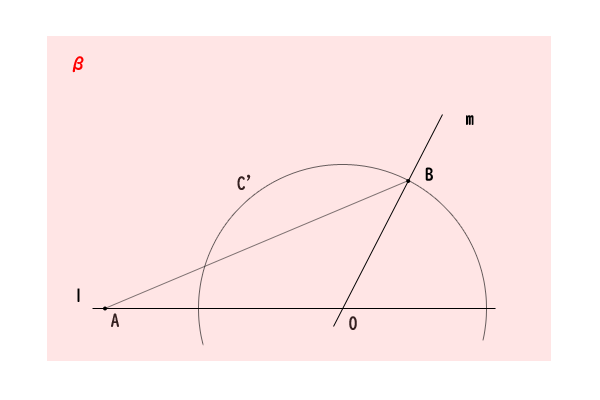
図12:平面\(\beta\)上に補助円\(c^{‘}\)を引く
平面\(\beta\)上で直線\(l\)と直線\(m\)の時計回りの角度を\(0^{\circ} \leq \phi \leq 180^{\circ}\)としましたが、同様に直線\(l\)と直線\(m^{‘}\)の時計回りの角度を\(0^{\circ} \leq \phi^{‘} \leq 180^{\circ}\)とすると、\(OB=OB^{‘}\)なので、平面\(\beta\)上の補助円\(c^{‘}\)に\(\angle AOB^{”}=\phi^{‘}\)となるように、点\(B^{”}\)を取ることができます。辺\(AO\)は共通で\(OB^{‘}=OB^{”}\)かつ\(\angle AOB^{‘}=\angle AOB^{”}\)なので、二辺挟角が一致し、三角形\(AOB^{‘}\)と三角形\(AOB^{”}\)は合同であることが分かります。
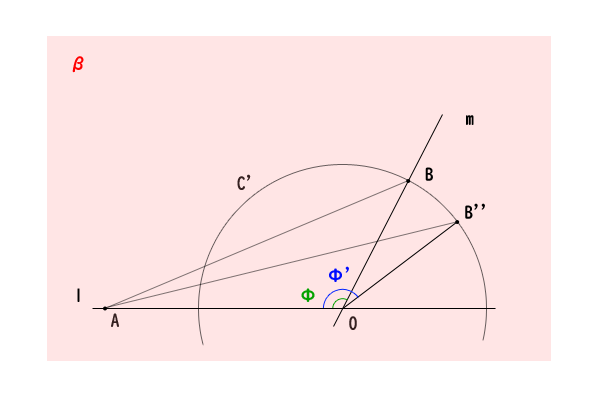
図13:平面\(\beta\)上の補助円\(c^{‘}\)に合同な三角形を取る
ここで、辺\(AO\)と補助円\(c^{‘}\)の交点を点\(H^{‘}\)とすると、中心角と弧の大小関係から\(\phi\ \lt\ \phi^{‘}\ \Rightarrow\ \stackrel{\frown}{H^{‘}B}\ \lt\ \stackrel{\frown}{H^{‘}B^{”}}\)が成り立ちます。
さらに、直線\(AB\)による補助円\(c^{‘}\)の位置関係を場合分けすると、①直線\(AB\)による補助円\(c^{‘}\)が接する場合、②直線\(AB\)による補助円\(c^{‘}\)が接しない場合に分けられ、②の場合はさらに、直線\(AB\)による補助円\(c^{‘}\)の弦を考えて点\(B\)と異なる補助円\(c^{‘}\)との交点を点\(C\)とすると、②-①弧\(CB\)の順番の場合、②-②弧\(BC\)の順番の場合に分けられます。
この場合分けに、\(\stackrel{\frown}{H^{‘}B}\ \lt\ \stackrel{\frown}{H^{‘}B^{”}}\)の場合の点\(B^{”}\)の位置を考慮すると、①の場合には、弧\(H^{‘}BB^{”}\)の順番であり、②-①弧\(CB\)の順番の場合には弧\(CBB^{”}\)の順番であり、②-②の場合には、さらに②-②-①弧\(BB^{”}C\)の順番と②-②-②弧\(BCB^{”}\)の順番に分けられます。
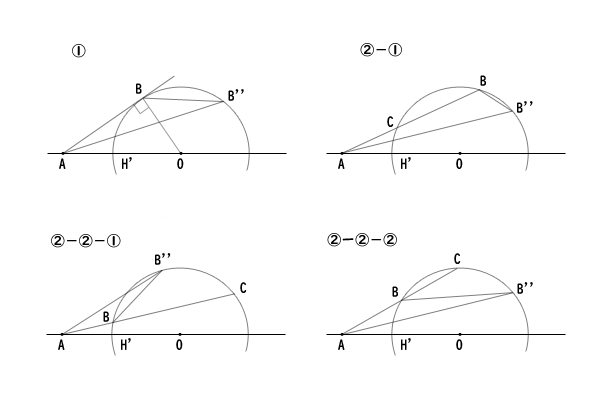
図14:点\(B,B^{”},C\)の位置関係による場合分け
①弧\(H^{‘}BB^{”}\)の順番の場合には、直線\(AB\)は補助円\(c^{‘}\)の接線なので、\(\angle ABO=90^{\circ}\)であり(参照:円と直線の距離と位置関係、特に交点、接点、接線について)、\(\angle ABB^{”}\)は鈍角であることが分かります。したがって、\(\angle AB^{”}B\)は鋭角なので、三角形の辺の長さと角の大きさの関係より、\(AB \lt AB^{”}\)であることが分かりました。
②-①弧\(CBB^{”}\)の順番の場合には、点\(B\)を含まない側の弧\(CB^{”}\)は半円よりも大きいので、円周角の定理より、\(\angle CBB^{”}\)は鈍角であり、したがって、\(\angle AB^{”}B\)は鋭角であり、やはり三角形の辺の長さと角の大きさの関係より、\(AB \lt AB^{”}\)であることが分かりました。
②-②-①弧\(BB^{”}C\)の順番の場合には、点\(B\)を含まない側の弧\(B^{”}C\)は半円よりも小さいので、円周角の定理より、\(\angle CBB^{”}\)は鋭角であり、したがって、\(\angle ABB^{”}\)は鈍角であり、\(\angle AB^{”}B\)は鋭角であり、やはり三角形の辺の長さと角の大きさの関係より、\(AB \lt AB^{”}\)であることが分かりました。
②-②-②弧\(BCB^{”}\)の順番の場合には、点\(B\)を含まない側の弧\(B^{”}C\)は半円よりも小さいので、円周角の定理より、\(\angle CBB^{”}\)は鋭角であり、したがって、\(\angle ABB^{”}\)は鈍角であり、\(\angle AB^{”}B\)は鋭角であり、やはり三角形の辺の長さと角の大きさの関係より、\(AB \lt AB^{”}\)であることが分かりました。
ちなみに、②-②弧\(BC\)の順番の場合で、点\(B^{‘}\)と点\(C\)が一致する場合は、三点が一直線上にあるので\(AB \lt AC = AB^{”}\)となります。
以上、すべての場合で、\(\stackrel{\frown}{H^{‘}B}\ \lt\ \stackrel{\frown}{H^{‘}B^{”}}\ \Rightarrow\ AB \lt AB^{”}\)であることが分かりました。
したがって、まとめると、
\[\phi\ \lt\ \phi^{‘}\ \Rightarrow\ \stackrel{\frown}{H^{‘}B}\ \lt\ \stackrel{\frown}{H^{‘}B^{”}}\ \Rightarrow\ AB \lt AB^{”} = AB^{‘} \]
が成り立ちます。
ここで、仮に\(AB \lt AB^{‘}\)のときに\(\phi^{‘}\ \lt\ \phi\)なる場合があったとすると、上記と\(\phi^{‘}\ \lt\ \phi\)より\(AB^{‘} \lt AB\)が成り立つので、\(AB \lt AB^{‘}\)であることと矛盾してしまいます。したがって、\(AB \lt AB^{‘}\)のときに\(\phi^{‘}\ \lt\ \phi\)なる場合はないので、\(AB \lt AB^{‘}\ \Rightarrow\ \phi\ \lt\ \phi^{‘}\)であることも分かりました。
したがって、すべてをまとめると、
\[\theta\ \lt\ \theta^{‘}\ \Rightarrow\ \stackrel{\frown}{HB}\ \lt\ \stackrel{\frown}{HB^{‘}}\ \Rightarrow\ HB\ \lt\ HB^{‘}\ \Rightarrow\ AB\ \lt\ AB^{‘}\ \Rightarrow\ \phi\ \lt\ \phi^{‘}\]
が成り立ちます。
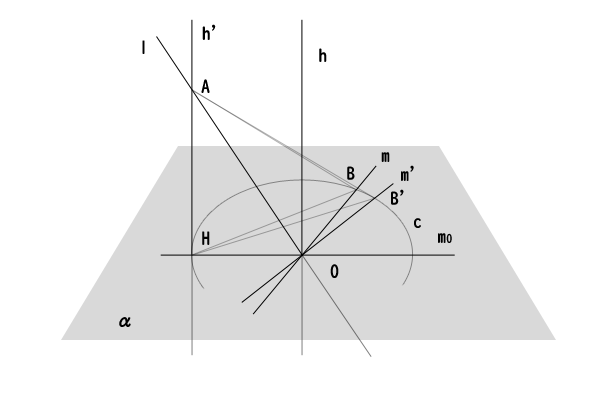
図15:\(\theta\)と\(\phi\)の大小関係の詳細を再確認
つまり、\(\theta\ \lt\ \theta^{‘}\ \Rightarrow\ \phi\ \lt\ \phi^{‘}\)を示すことができました。
ここで\(\theta\)の最小値は\(0^{\circ}\)なので、\(\phi\)の最小値は\(\theta=0^{\circ}\)のとき、つまり、直線\(m_{0}\)のときであることが示せました。□
試みの結果
ここまで論理的な証明を眺めてきて、直線と平面のなす角に関する直観的なイメージは豊かになったという実感はありますでしょうか。最後に、このページを見ずに「直線と平面のなす角」という言葉からどれだけ幾何学的事実を直観的に思い描けるかを試してみて、始めに持っていたイメージと比較してみて下さい。
もしも、より多くの事実を描き出すことができるようになっていて、その原因が以上の論理的な証明を読んだことにあると実感できるのであれば、この勉強法を続けてみてください。そのような実感がないのであれば、残念ながらその方にはこのような勉強法がそれほど合わなかったのだと思います。あまりこのページで説明した論理的な方法に固執せずに、別の自分に合う勉強法がきっとあるのではないかと思います。それぞれ独自の勉強法が、個性的な数学や科学を展開する根源にあることを忘れず、自分の持つ個性を大切にしなければならないと思います。
理数系科目の習得に限界を感じ、論理学、数理論理学、数学基礎論、その他哲学の本に手を伸ばして、それらの細かな知識をたくさん知ったとしても、もちろん、分野毎に必須の形式化された手法というのは色々とあり重要ですが、それも実際の勉強や研究において生きるのは、特に発見や創造において生きるのは、各分野の原理部分に限られる場合が多いと思いますし、さらに、基本的で繰り返し用いる応用範囲の広い論理に限ったとすると、デカルトの指摘したように必要な規範はとても少なく、基本の論理としては、このページで示した上記①~④(①疑問を持って根拠を求め、逆に、正しい推論を行う、②推論から矛盾を排除する、③推論の順序や重要度を意識する、④すべてを考えに含めて漏れを許さない)で十分で、⑤~は発展的な内容になるくらいかと思います。
このページで示した上記①~④のように、たわいなくさえ見える単純な論理的な原則を使いこなせるようになって、コツコツと論理的な考察を伴った勉強を行い、物事の直観的な理解を深めていくことが大切だと私は思っています。
それがいざ、様々な分野の実践で即断を求められたときであっても、磨き上げた単純な論理的思考と訓練で培った豊かな直観的理解が多いに役立つはずです。このような訓練を意識的に積んでいない人からは、不思議に感じられるほどの能力開発にも繋がっていくだろうと思います。
もちろん、正確な判断のためには論理的で慎重な考察が必要になりますが、常に時間に溢れているわけではありません。論理的な考察で直観的な理解を豊かにしておくことが大切になると思います。
著者:L&M個別オンライン教室 瀬端隼也
公開日:2020年1月21日
修正日:ー



※このサイトはreCAPTCHAによって保護されています。そのためGoogleのPrivacy PolicyとTerms of Serviceが適用されます。