平面に垂直な直線(平面に直交する直線、垂線)について
【目次】
1.直線と平面の「垂直、直交、垂線」の定義
2.直線と平面の「垂直、直交、垂線」の証明
3.余談:暗記と論証の違い
直線と平面の「垂直、直交、垂線」の定義
数学Aの教科書(数研出版、高校数学の教科書、以下同じ。詳しくは、高校数学マスター基本方針:参考にする教科書を参照ください)では、直線と平面の「垂直、直交、垂線」を次のように定義しています。
【定義:直線と平面の「垂直、直交、垂線」】
直線\(l\)が、平面\(\alpha\)上のすべての直線に垂直であるとき、直線\(l\)は\(\alpha\)に垂直である、または、\(\alpha\)に直交するといい、\(l\perp \alpha\)と書く。また、このとき、\(l\)を平面\(\alpha\)の垂線という。
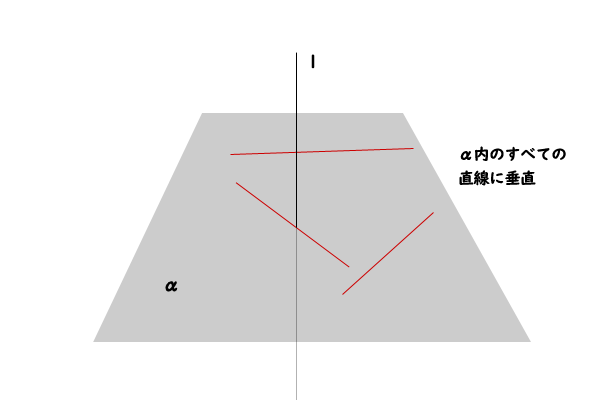
図1:直線と平面の「垂直、直交、垂線」の定義
その上で、平面に対して垂線となるための十分条件として、次の命題を紹介しています。
【命題:平面の垂線の十分条件】
直線\(l\)が、平面\(\alpha\)上の交わる2直線\(m,n\)に垂直ならば、直線\(l\)は平面\(\alpha\)に垂直である。
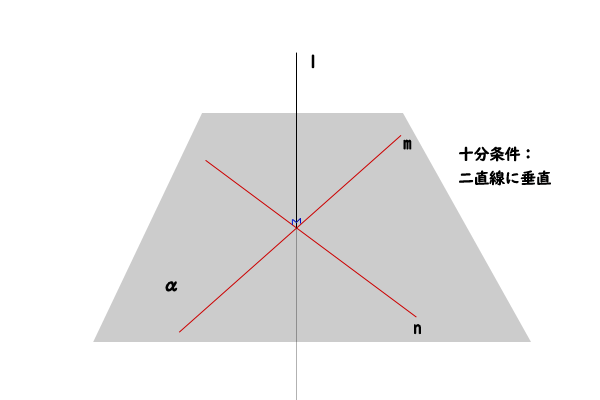
図2:平面の垂線の十分条件
しかしながら、教科書においては、命題を紹介するのみで証明が省かれていますので、このページではきちんと証明を行いたいと思います。【命題:平面の垂線の十分条件】の証明は、ユークリッドの原論に素晴らしい証明が掲載されていますので、そちらを基本的に紹介していきたいと思います。
直線と平面の「垂直、直交、垂線」の証明
【証明】
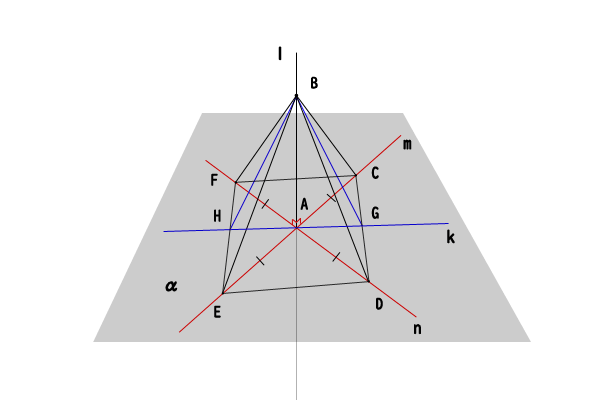
図3:平面の垂線の証明
まず、直線\(l\)と2直線\(m,n\)が交わる点を交点\(A\)とします。そして、平面\(\alpha\)上の点\(A\)を通る任意の直線を直線\(k\)とします。
それでは始めに、直線\(l\)と直線\(k\)が直交することを証明したいと思います。
直線\(l\)上に点\(A\)ではない点\(B\)を取ります。2直線\(m,n\)上に時計回りに、点\(C,D,E,F\)を\(CA=DA=EA=FA\)となるように取ります。ただし、直線\(m\)上の点が点\(C,E\)、直線\(n\)上の点が点\(D,F\)とします。
ここで、直線\(k\)が線分\(CD\)を通ることとします。それ以外の場合は線分\(DE\)を通りますが、証明は同様に行うことができます。直線\(k\)と線分\(CD\)の交点を点\(G\)、直線\(k\)と線分\(EF\)の交点を点\(H\)とします。
そこで目標としては、\(\angle BAG = \angle BAH\)を示し、直線の角度\(180^\circ\)の半分だから\(\angle BAG = \angle BAH =90^\circ\)であることを示して、直線\(l\)と直線\(k\)が直交することを証明したいと思います。
証明の方針としては、三角形の合同を次々に適用していきます。平面において成り立つ法則を組み合わせて空間に成り立つ法則を導き出す、部品から全体を組み立てるような、これぞ立体図形の証明という感じです。
三角形\(CAD\)と三角形\(EAF\)について、\(CA=DA=EA=FA\)かつ\(\angle CAD = \angle EAF\)より、三角形\(CAD\)と三角形\(EAF\)は合同です。
三角形\(CAG\)と三角形\(EAH\)について、\(CA=EA\)かつ\(\angle CAG = \angle EAH\)、上記より\(\angle ACG = \angle AEH\)であり、二角狭辺が等しいので、三角形\(CAG\)と三角形\(EAH\)は合同です。
したがって、\(GA = HA\)であることが分かりました。
次に、三角形\(CBA\)と三角形\(EBA\)について、\(BA\)が共通の辺、\(CA=EA\)、直線\(l\)と直線\(m\)は直交するので\(\angle CAB = \angle EAB = 90^\circ\)より、二辺挟角が成り立つので、三角形\(CBA\)と三角形\(EBA\)は合同です。
同様にして、三角形\(DBA\)と三角形\(FBA\)も合同です。
したがって、\(CB=EB\)、\(DB=FB\)が分かりました。
ここで、三角形\(CDB\)と三角形\(EFB\)について、\(CB=EB\)、\(DB=FB\)、くわえて先ほど示した三角形\(CAD\)と三角形\(EAF\)は合同であることから、\(CD=EF\)なので、三辺が等しいことが分かり、三角形\(CDB\)と三角形\(EFB\)が合同であることが分かります。
そして、三角形\(CBG\)と三角形\(EBH\)について、\(CB=EB\)、三角形\(CAG\)と三角形\(EAH\)が合同なので、\(CG=EH\)であり、さらに三角形\(CDB\)と三角形\(EFB\)が合同なので、\(\angle BCG = \angle BEH\)なので、二辺挟角が成り立つので、三角形\(CBG\)と三角形\(EBH\)が合同であることが分かりました。
したがって、\(BG=BH\)が成り立ちます。
そうすると、最後に三角形\(ABG\)と三角形\(ABH\)について、\(GA = HA\)、\(BG=BH\)、さらに\(AB\)を共有しているので、三辺が等しく、三角形\(ABG\)と三角形\(ABH\)が合同であることが分かりました。
したがって、\(\angle BAG = \angle BAH\)であり、直線の角度\(180^\circ\)の半分だから\(\angle BAG = \angle BAH =90^\circ\)なので、直線\(l\)と直線\(k\)が直交することが示せました。
さらに仕上げとして、平面\(\alpha\)上の任意の直線を直線\(j\)とすると、平面\(\alpha\)内で点\(A\)を通り直線\(j\)に平行な直線\(j^{‘}\)をただ一つ引くことができます。
これまでの証明より、直線\(k\)を直線\(j^{‘}\)と置き換えれば、直線\(j^{‘}\)は直線\(l\)と直交することが分かります。
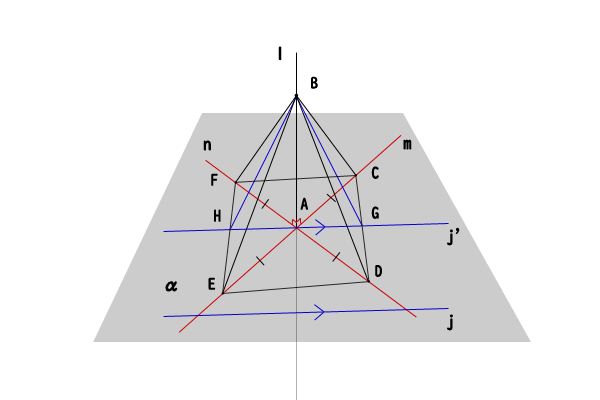
図4:平面\(\alpha\)上の任意の直線に垂直
空間における2直線なす角は、空間内の任意の点を通るその2直線に平行な2直線のなす角によって定義されており、任意の点においてその平行な2直線のなす角は等しいのでした。(参照:空間図形における二直線のなす角と二平面のなす角)
したがって、少なくとも一つの点\(A\)において直線\(j^{‘}\)と直線\(l\)が直交することを示したことで、空間内の任意の点においても同様であり、空間における2直線のなす角の定義より、直線\(l\)と直線\(j\)が直交することを十分に示すことができました。
以上より、平面\(\alpha\)上の任意の直線と直線\(l\)は直交するので、【定義:直線と平面の「垂直、直交、垂線」】より、直線\(l\)と平面\(\alpha\)が直交することが示されました。□
余談:暗記と論証の違い
本節の前提として高校数学の教科書は、当世の最も優れた数学者や数学の先生方で入念に執筆され、高校生の学力に合わせて作成された高い水準の教本となっていることは知っておかなければなりません。しかし一方で、学校制度の下で標準的に頒布されるために作成され、そのための様々な制約を守ってその内容を執筆していることも知らなければなりません。つまり、高校数学の教科書は、かなり強い制約の下に標準を目指して書かれた教科書であって、決して標準ではないすべての学生にとって、良い教科書ですが最適な教科書とは言えないのです。
ここからは、真剣に学ぼうとしている学生にとっては有益な情報となると思いますので、気が進みませんが若干の苦言を述べると、高校数学の教科書を読む学生は、数学というものにまだ不慣れで論理や証明という数学の基本にも習熟していません。そのため、ほとんどの昨今の高校数学の教科書のように、「これは成り立つ」の一言で「証明は簡単である。」の一言さえもない文章は、数学を嫌煙しないようにするための恩情なのかもしれませんが、逆に、多くの学生に数学という学問に対する誤解を与え、その入門を阻害している一大要因になっていると感じます。
すべての学生が数学の教科書を読むにあたり知っておくべき最低限の基礎知識は、数学の教科書に載っているすべての記述、主張は、「証明なしに認める」か「証明がある」のいずれかに該当するということです。したがって、「証明なしに認める」という記述がなく、証明が載っていない主張については、すべて証明が省略されているということです。つまり、自分で考えるか調べるかすれば証明があるということです。
良書と言えるような数学の教科書であれば、「これは明らかである。」の一言くらいは記述され、証明を省略することを暗に示します(ただ、たまに「証明なしに認める」の意の場合があります)。つまり、このくらいのことは自分で考えるか、調べてください、という意味が含まれます。丁寧な数学の教科書では、それなりの証明を省く場合には「証明が煩雑な割に本筋と関係ない」「紙数が足りない」等の証明を省く理由や参考文献を紹介するくらいのことは行います。それらは、その教科書の想定する読者の力量に合わせた記述が取られることになるわけです。
つまり、本当であれば、行間や慣習を知らない読者で力量が低ければ低いほど、その説明は冗長であっても丁寧に行うべきなのが誠実さというものです。すべての高校教師に一々このような事実を口頭で述べるように依頼しているわけではないのですから、教科書の表現を工夫するか、少なくともまとめてこのような説明を付け足す配慮は必要なのだろうと思います。
もちろん、数学に興味のある学生は、勝手に数学における良書を探し出し、このようなことを気にすることもなく自然に学んでいくと思います。しかし、そうでない学生は、大学で理数系、特に数学科に入ることもないと思いますので、運の悪いことに一生の間で丸暗記と論証(議論)の区別が判然としないような幼児相手の数学教育しか受けられないという悲劇が生じているのではないかと思います。
大まかな話ですが、数学の得意な学生は、行間に省略された証明を補いながら教科書を読んでおり、そうでない学生は、その証明を補わずに教科書を読んでいます。どこまで深く証明を考えながら、そして、それなりに早く効率的に読めるかが、学生や学者の区別なく数学の実力に直結しているのではないかと感じます。
「これは明らかである。」という言葉は、「全然、明らかじゃないよ」という反発を招くかもしれませんが、このような丸暗記と論証の違いに気付くための、最低限の扉として高校数学の教科書の中にも準備されておくべきではないかと感じます。もちろん、学生の力量を考えれば「証明は簡単なので省きます」、「証明は長いので省きます」、「証明は難しいので省きます」などと省略する理由を言明する方が良いだろうと思います。
特に、文化的に日本の一般的な学生は、議論による説得なしに既成の主張を鵜呑みにしがちである、あるいは、暗記と論証による理解の違いを判別するのが得意でない、と長らく指摘されてきているわけですから、数学教育ひいては論理教育の柱である高校数学の教科書においては、特段の配慮が求められるべきだと思います。それは、教育と学問の境目ではなく、幼児教育と普通の教育(人対人の教育)の境目をどこにおくべきかという問題であると感じます。
大げさな話ですが、すべての国民が通る高校数学の教科書がきちんとした論理教育の柱となれば、労働生産性の向上や社会各所の合理化などに多大な貢献をし得ると、その可能性を感じたからこそ、この高校数学マスターを作成しています。注記なくほとんど論証のないユークリッド幾何学の立体図形が高校数学の教科書で展開されていることに驚き、少なからぬ不安と戸惑いを感じたので、迷いましたが余談として付記しました。考える力を付けるための教育改革を行うのであれば、おそらく今後、高校数学の教科書は、多大な労力をかけた改定を行う必要があると感じます。
つまり、将来どのような知識が必要となるかを予想して優先順位を付けて知識を教科書に詰め込むだけではなく、将来必ず必要となる理解や能力、つまり、数学や学問に対する理解や論理的な能力を養成すること、それらを最低限かつ重点目標とする構成に変更するべきでしょう。例えば、経済的問題もあるかと思いますが、論証に力を入れた基本的な教本と、網羅的な知識について証明をきちんと掲載した資料集の二段構えなどはどうだろうかとも漠然と思います。もちろん、検証を踏まえた漸次的な変更が望ましいと思います。
ただ、残念ながら、歴史的文化的な背景を含めて、我が国は教育学問において決して先進的な国ではなく、学校、受験、大学、官僚、政治、様々な教育に関わる制度に課題を抱えていますので、恐らくそれほど改善をもたらす教育改革を行うことはできないだろうとも思います。何より、国全体としてどうこうというのが必ずしも正解ではありません。もちろん、それは尊い貢献ですが、少し経験を積んで世界をよく見回せば、理想的な国など過去にも現在にも一つもないことが分かると思います。
少なくとも現在の日本は、過去に比べて、各個人が最善の知識を求めていけば、それに見合うだけの成果を得られる平和で恵まれた国であることだけは確かであり、その最も尊い価値を忘れてはいけないと思います。恐れるべきは、その恩恵を生かすことのできない各々の力不足だろうと自戒しています。つまり、学生個人としては、高校教育に飽き足らなければ放課後にそこかしこにある立派な図書館に行けば済む話です。そして、ユークリッドの原論等の良書を探し求め、親しむ習慣を身に付けることです。
著者:L&M個別オンライン教室 瀬端隼也
公開日:2019年12月18日
修正日:ー



※このサイトはreCAPTCHAによって保護されています。そのためGoogleのPrivacy PolicyとTerms of Serviceが適用されます。