図形と方程式、点と直線のポイント解説9選
【目次】
0.はじめに
1.直線上の点と実数の対応
2.線分の内分点と外分点
3.線分の内分点と外分点、座標とベクトルへの応用
4.平面座標上の直線の方程式
5.\((x_1,y_1)\)を通る直線の方程式
6.垂直条件\(m_1\cdot m_2 = -1\)の証明
7.点\(x_1,y_1\)を通り、直線\(ax+by+c=0\)に平行な直線、垂直な直線
8.2直線の関係と連立一次方程式の解
9.座標を使った三角形の垂心の存在証明
はじめに
高校数学の教科書(詳しくは、高校数学マスター基本方針:参考にする教科書を参照ください。以下同じ。)の数学Ⅱ第3章「図形と方程式」の重要性は、記事「図形と方程式とデカルト、高校数学と科学の基礎について」でも解説しましたが、現代の数学や科学の屋台骨と言って良いほどの重みを持っています。したがって、できるだけ基礎を深く理解することでこの先の数学や科学への導入が心地良いものになると思います。
そこでこのページでは、数学Ⅱ第3章「図形と方程式」第1節「点と直線」の疑問を持ちそうな未消化になりがちなポイントを丁寧に解説していきたいと思います。
直線上の点と実数の対応
教科書のp.64(教科書番号709ではp.72)の本章の冒頭は次のような下りから入ります。
数直線上では、点Pに一つの実数aが対応している。このとき、aを点Pの座標といい、座標がaである点PをP(a)で表す。
とてもシンプルで良い文章です。このような文章をどこまで深くじっくりと自分の頭で考えられるかが後々に勉強がスムーズに進むか否かの一つの分かれ目になるのかなと思います。ほとんどの若い方は読み飛ばして先に進んでしまうのではないでしょうか。そこを我慢して思慮深くあるべく、一緒に考えてみましょう。
まず、上記の記述は「座標」を定義しているわけですが、通常、座標と言われて思い浮かべるのは2次元平面座標ではないでしょうか?そこを上記定義は、1次元直線座標から定義を始めているのです。つまり、1次元直線座標をきちんと定めて考察すれば、それが2次元平面、3次元立体の座標の元になると著者たちが考えていること、そして、そのように考察を進めていく構成にこの教科書はなっているのだなと予想することができるのです。
例えば、上記では座標aである点をP(a)で表す、としていますが、それが2次元平面座標ではP(a,b)、3次元立体座標ではP(a,b,c)と書けばよいだろうと予測が付きますし、点と数の組の対応が一目で分かり、なかなか便利そうな記述法だと考えるわけです。
そして、次に、しっかりと定義の内容を吟味してみるのです。「数直線上では、点Pに一つの実数aが対応している。」とはどういうことかと。数直線とは、単なる直線ではなく、実数が対応している直線であり、かつ、一つの点に一つの数が対応しているものだということがここから読み取れます。
ここで沢山の疑問が生まれるでしょう。例えば、点、直線とは何なのか?実数とは何なのか?これらの対応関係とは何なのか?と。そうしたら少し教科書を閉じて、数時間でも数日でもゆっくりと(ぼんやりと何気なく)自分の頭で考えてみることをお勧めします。この定義に間違いはないのか?合理的な理由があるのだろうか?と。
そこで、次のような考えを感覚的にでも掴むことができれば、かなりその後の数学の勉強が楽しくなるはずです。その考えとは、幾何学的な点、直線といっても絵にして描けばそこに幅や長さがある。教科書で用いられている点、直線という言葉はもっと現実的な認識を理想化した、「幅や長さのない点」や「幅のない線」を考えている。つまり、図形といってまるで目に見えているものを扱っているようだけれども、実際の点や線は目に見えないものなのだ。なぜなら幅や長さが点にあったならその中にさらに小さな本当の点があるはずだし、かといって、幅や長さがなければ目に見えるはずがないと。
実際、図形として描いた目に見える点や線は、その目に見えないはずの概念を表すための記号に他ならないわけです。ただ、その概念が目に見えないから意味がないかというとそうではなくて、逆に、現実に存在する物体の図形を考える際に大変重宝する、とても便利な概念になっているわけです。
これは数についても同様のことが言えます。1,2,3,…と書く自然数はあくまで記号であって、そこには目に見えない、けれど、この自然に存在する多くのものに共通する概念としての自然数があるわけです。つまり、共通する概念として、リンゴの山でもお金の山でも区別なく、自然数によって、数を数えることができるわけです。しかも、リンゴの山もお金の山も目には見えますが、それが持っている何個・何円という共通する概念(特徴)は、実際には目には見えないのです。
簡単に言うと、点や線、数を知らない人や動物が見てもそこには点や線、数はないわけです。ただ、知っている人だけがいつの間にか見えている気になっているわけです。あるいは、先人が苦労して発見したその概念をたしかに学んで便利に利用することができているのです。
図形と数というその二つの概念を上記の定義では、「点Pに一つの実数aが対応している」と記号Pやaを使うことで対応させています。それも自然数では、数直線上に自然数に対して対応が付けられない点が出てしまう、という研究がなされた上で、さらに自然数と自然数の割り算である有理数でもやはり、数直線上に有理数に対して対応が付けられない点が出てしまう、という研究がなされた上で、そして、結局、実数であれば数直線上にある無数の点と一対一の対応が付けられるという研究がなされた上で、このような定義となっています。
そこには、数学Ⅰのp.27で学んだように、ピタゴラスの時代に\(\sqrt{2}\)の長さの直線が発見された瞬間から始まる長い研究の歴史があります。
最後に以上を整理して正確に考えるために、数学Ⅰのp.44で学んだ集合の概念を使って冒頭の定義を捉え直しましょう。つまり、直線という全体集合を持つ点の集合と、実数という全体集合を持つ数の集合が、一つの点と一つの数で対応関係を持つ、その対応関係を点P(a)あるいは点Pの座標aと呼ぶという定義をしていることが分かります。
このように考えを進めることが深く考えるということの一例で、実際には言語化が進まなくとも初めて学ぶ時には初めてなりにイメージを膨らませる時間を持つことが大切です。初めは誰もが上手く行きませんが、付かず離れず楽しみながら考える習慣が付くと、だんだんと深く考えるということができてきて、そうして正しくかつ自分だけのアイデアというものが生まれていきます。
ちなみに、先程の点と線についての考察の中で出てきた「見える見えない」「幅や長さはあるのかないのか」などの疑問は、そのまま物理学への入門にもなっていきます。つまり、見えるとは何なのか、光とは何なのか、光が粒子なら直径はあるのか、など疑問は尽きないはずです。
線分の内分点と外分点
数学Ⅱのp.65では、線分の内分点と外分点を解説しています。どちらも線分ABを比m:nで内分あるいは外分した点Pの数直線上の座標を求めることで一致しています。
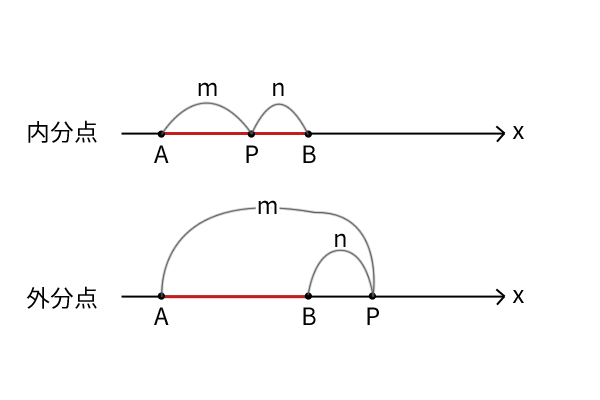
図1:線分の内分点と外分点
注意点は、まず数直線上の点Aと点Bの位置関係を把握すること、次に比m:nが点Pと点Aを結んだ線分APあるいは点Pと点Bを結んだ線分BPのどちらと対応するのかを把握することです。点Aと点Bの位置関係は逆になることがあります。一方で、点Aと点Bの位置が逆であろうがなかろうが、比のmは線分APに対応し、nは線分BPに対応します。
内分点と外分点の違いは、内分点は線分ABの中に点Pがあること、外分点は線分ABの外に点Pがあることです。さらに、外分点のときには、点Pが線分ABの左か右のいずれかにある場合に分かれますが、位置が左でも右でも比のmが線分APに対応し、nが線分BPに対応することは変わりません。ちなみに、教科書では外分点はPではなくQと記載しています。
このように対応させると、内分点の点Pの座標xは、
\[x=\frac{na+mb}{m+n}\]
となるのでした。証明は、比m:nと対応する線分APと線分BPの長さの比を等式に取り、\(a>b\)のときは\(m:n=(x-a):(b-x)\)、\(b>a\)のときは\(m:n=(a-x):(x-b)\)より計算すれば出るのでした。
内分点は、上記のように座標と反対の比を掛けるだけと考えると公式も覚えやすく、使っている間に自然と覚えてしまうと思います。
一方で、外分点の公式は、
\[x=\frac{-na+mb}{m-n}\]
と一見すると、マイナスが入って各点や比の位置関係によってマイナスが動きそうで混乱しそうです。けれど、実際には、分子と分母の両方にマイナスを掛けても等しいので、
\[x=\frac{-na+mb}{m-n}=\frac{na-mb}{-m+n}\]
が成り立っています。
証明は、内分点と同様に比m:nと対応する線分APと線分BPの長さの比を等式に取るという基本は変わりませんが、外分点の場合は比m:nの大小関係で点Pの線分ABに対する位置が逆になるので、場合分けの数が増え、\(a>b\)かつ\(m>n\)、\(a>b\)かつ\(m < n\)、\(a\ < b\)かつ\(m>n\)、\(a\ < b\)かつ\(m\ < n\)の4つの場合を考える必要があります。教科書はおそらく紙数の制限で場合分けを省略していますが、一度きちんと証明を頭でも良いのでなぞってみると良いと思います。
そうすると、教科書にも書いてある通り、4つの場合に関係なくすべての場合において上記の公式が成り立つのでした。結局、座標と反対の比を掛けることは内分点の公式と同じで、比のmかnのどちらかをマイナスにすれば良く、それはどちらでも良いわけです。そうすると、外分点の公式も使いやすく感じるのではないでしょうか。
以上のように、疑問を持って、自分の頭で教科書の行間を埋めながら勉強することが理解を深めていくことにつながると思います。あとは、例えば数の組(m,n)がどんな値を取ることができるのか、それに伴い\(\frac{m}{n}\)はどう動けるのか、などと考えてみることも内分点や外分点の理解と共に、比や分数、そして有理数や数、数の組などの理解も深めてくれると思います。
線分の内分点と外分点、座標とベクトルへの応用
前章では、1次元数直線上(1次元直線座標上)の線分の内分点と外分点の座標を求めました。数学Ⅱのp.69では、次に2次元平面座標上の線分の内分点と外分点の座標を求めています。
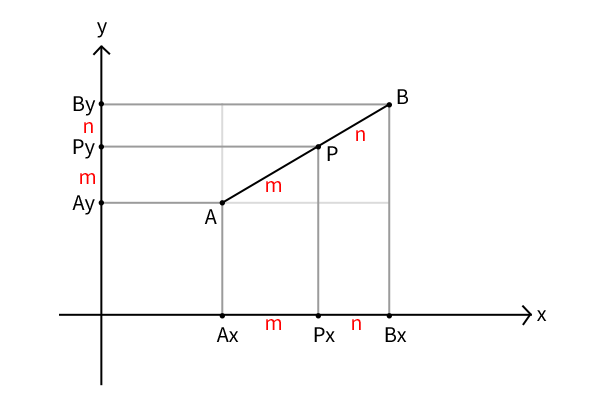
図2:2次元平面座標上の線分の内分点
証明は、上図のように各点の座標を各軸の一直線上で考えて、比m:nが平行線によって保存されることから、前章の1次元直線座標上の証明を各xy座標について再適用することに帰結すれば良いわけです。つまり、各点\(A(x_1,y_1),B(x_2,y_2),P(x,y)\)とすると、内分点は、
\[(x,y)=(\frac{nx_1+mx_2}{m+n},\frac{ny_1+my_2}{m+n})\]
となり、外分点は、
\[(x,y)=(\frac{-nx_1+mx_2}{m-n},\frac{-ny_1+my_2}{m-n})\]
となります。ここまでが教科書の解説です。さらに、同様の考え方は3次元立体座標上の線分の内分点と外分点の座標についても適用できるという指摘をしておきたかったことが一点と、あと、以下のようにベクトルの内分と外分にも応用できることを指摘しておきます。
外分の式変形も同様ですので、ここでは内分のみ取り上げます。また、ベクトル\(\vec{v_1},\vec{v_2},\vec{v}\)は各点A,B,Pの位置ベクトルとしましょう。
\[\vec{v}=(x,y)=(\frac{nx_1+mx_2}{m+n},\frac{ny_1+my_2}{m+n})=(\frac{n}{m+n}x_1 + \frac{m}{m+n}x_2,\frac{n}{m+n}y_1 + \frac{m}{m+n}y_2)\]
\[=(\frac{n}{m+n}x_1,\frac{n}{m+n}y_1) + (\frac{m}{m+n}x_2,\frac{m}{m+n}y_2)=\frac{n}{m+n}(x_1,y_1)+\frac{m}{m+n}(x_2,y_2)\]
\[=\frac{n}{m+n}\vec{v_1}+\frac{m}{m+n}\vec{v_2}=\frac{n\vec{v_1}+m\vec{v_2}}{m+n}\]
結局、多次元やベクトルにおいても1次元数直線上の証明が基本になっています。したがって、基本が大切ということも言えますが、分からなければ基本に戻ることの大切さを感じられるかと思います。
平面座標上の直線の方程式
数学Ⅱのp.72では、一次方程式\(ax+by+c=0\)が平面座標上で直線になることを示しています。逆に、平面座標上の直線は、一次方程式\(ax+by+c=0\)で表されることにも言及していますが、証明は省略されています。そこで、きちんと証明をしておきたいと思います。
「平面座標上の一般の直線」というように少し漠然とした対象を明確に考えていくための一つのコツは、考慮すべきすべての対象に共通の特徴を見つけることです。そうすると、漏れなくすべての対象を扱うことができ、さらにその特徴で分類していくことができます。
「平面座標上の一般の直線」であれば、どんな直線にも一定の傾きがあることが分かります。逆に、一定の傾きがない曲線は直線とは言えません。これにより漏れなく直線を扱うことができます。さらに、一定の傾きで分類をしていきたいと思います。
特別な傾きが二つあります。x軸に平行な直線とy軸に平行な直線です。前者の傾きは\(0\)で後者の傾きは\(\infty\)と言って良いでしょう。その他の直線の傾きは、それ以外の実数の値を持っています。
ただ、傾きだけでは直線を一つに確定できませんし、したがって一次方程式\(ax+by+c=0\)で表すこともできません。少し注釈を入れると、一次方程式\(ax+by+c=0\)のa,b,cは定数で座標上で動かさない数、x,yは変数で座標上で動かす数なのでした。もちろん、場合分け等のために定数a,b,cを動かしてみることもありますが、あくまでも特別な場合であって方程式の表す曲線との区別を付ける必要があります。定数はアルファベットの先頭、変数はアルファベットの後尾を使う習慣によってこれが分かるのでした。
そうすると次に、傾きを確定した直線の中で共通の特徴を探すと、それはx切片(x軸との交点)かy切片(y軸との交点)を必ず持つということです。x軸に平行な直線はy切片のみを持ち、y軸に平行な直線はx切片のみを持ち、それ以外の直線はx切片もy切片も持ちます。
そして、x切片かy切片のいずれかが定まれば直線を一つに確定することができます。それでは、確定したすべての直線について一次方程式\(ax+by+c=0\)で表されるかを考えてみましょう。
x軸に平行な直線は、\(y=c\)と表すことができます。\(a=0,b=1\)ということです。
y軸に平行な直線は、\(x=c\)と表すことができます。\(a=1,b=0\)ということです。
それ以外の直線は、傾きをd、y切片をeとすれば、\(y=dx+e\)で表され、変形すると\(-dx+y-e=0\)なので、\(a=-d,b=1,c=-e\)と置けば一次方程式\(ax+by+c=0\)で表されることが分かりました。
したがって、平面座標上のすべての直線が一次方程式\(ax+by+c=0\)で表されることを示せました。□
一次方程式\(ax+by+c=0\)(ただし\(a\neq 0\)又は\(b\neq 0\))は平面座標上の一つの直線を表し、平面座標上のすべての直線は一つの一次方程式\(ax+by+c=0\)(ただし\(a\neq 0\)又は\(b\neq 0\))で表されるので、一次方程式\(ax+by+c=0\)(ただし\(a\neq 0\)又は\(b\neq 0\))と平面座標上の直線は一対一対応であることが分かります。集合のベン図を使って確認してみて下さい。
ちなみに、\(a\neq 0\)又は\(b\neq 0\)の否定である\(a=0\)かつ\(b=0\)の場合にどうなるかというと、\(ax+by+c=0\)に代入して\(c=0\)が求められ、したがって、\(0\cdot x+0\cdot y+0=0\)が成立します。つまり、数の組\((x,y)\)はすべての実数の組を取ることができます。それは直線でも曲線でもなく、平面一面ということになります。
\((x_1,y_1)\)を通る直線の方程式
数学Ⅱのp.73では、点\((x_1,y_1)\)を通る直線の方程式\(y-y_1=m(x-x_1)\)を導き出していますが、証明が少し曖昧なので、ここではきちんと証明したいと思います。
点\((x_1,y_1)\)を通る直線の方程式を定数m,nを定めて\(y=mx+n\)としましょう。そうすると、点\((x_1,y_1)\)を通るので、座標\((x_1,y_1)\)を代入して、
\[y_1=mx_1+n\]
が成り立ちます。これを方程式\(y=mx+n\)から差分した
\[y-y_1=m(x-x_1)\]
も成り立ちます。したがって、点\((x_1,y_1)\)を通る傾きmの直線(以下、これを直線\(l\)としましょう)ならば、言い換えると、直線\(l\)上にある点の座標ならばすべて方程式\(y-y_1=m(x-x_1)\)を満たすことが分かりました。ただ、ここまででは、逆に方程式\(y-y_1=m(x-x_1)\)を満たす座標の点が直線\(l\)を表す(正確には、直線\(l\)に含まれる)とは言及していません。
方程式\(y-y_1=m(x-x_1)\)を変形すると\(-mx+y+(-y_1+mx_1)=0\)あるいは\(y=mx+(-mx_1+y_1)\)となります。前章において、一次方程式\(ax+by+c=0\)はxy平面座標上の直線と一対一対応であることを示しましたので、方程式\(y-y_1=m(x-x_1)\)も一つの直線と対応することが分かります。
仮に、直線\(l\)以外の直線\(L\)と対応するならば、方程式\(y-y_1=m(x-x_1)\)は二つの直線\(l,L\)を含むことになり、一つの直線と対応することに矛盾してしまいます。したがって、方程式\(y-y_1=m(x-x_1)\)が直線\(l\)を表すことを示せました。□
ちなみに、上記は傾きmが実数の場合であり、y軸に平行な場合には\(x=x_1\)となります。
垂直条件\(m_1\cdot m_2 = -1\)の証明
数学Ⅱのp.75では2直線の平行と垂直の条件を示しています。つまり、2直線の傾きを\(m_1, m_2\)とすると、平行の場合は\(m_1= m_2\)、垂直の場合は\(m_1\cdot m_2 = -1\)が成り立ちます。前者は分かりやすいと思いますが、後者には証明が必要で教科書の証明は、発想がなかなか勉強になる方法を取っています(教科書番号709ではp.83に同じ証明が掲載されています)。
ここでは、数学B第一章「平面上のベクトル」で学ぶ内積を用いた証明を行いたいと思います。どんな公式も色々な見方、色々な分野とのつながりを知ることで理解が深まり、使いやすく忘れにくくなるからです。
垂直な2直線に各々平行なベクトル\(\vec{a},\vec{b}\)、その成分をそれぞれ\(\begin{pmatrix}x_1 \\ y_1\end{pmatrix}\)、\(\begin{pmatrix}x_2 \\ y_2\end{pmatrix}\)としましょう。ベクトルの内積は、
\[\vec{a}\cdot \vec{b} = |\vec{a}||\vec{b}|cos\theta\]
と定義されるのでした。したがって、垂直条件が
\[\vec{a}\cdot \vec{b} = |\vec{a}||\vec{b}|cos90^\circ =0\]
と出て、一方で余弦定理より、内積の成分表示は、
\[\vec{a}\cdot \vec{b} = |\vec{a}||\vec{b}|cos\theta = x_1 x_2 + y_1 y_2\]
となるのでした。両者を合わせて、内積の垂直条件は、
\[x_1 x_2 + y_1 y_2 = 0\]
と導かれるのでした。変形すると、
\[\frac{y_1 y_2}{x_1 x_2} = -1\]
となります。さらに、次のように見ることができます。
\[\frac{y_1 y_2}{x_1 x_2} = \frac{y_1}{x_1}\cdot \frac{y_2}{x_2}\]
ここで、\(\frac{y_1}{x_1}\)はベクトル\(\vec{a}\)の傾きで、ベクトル\(\vec{a}\)は傾き\(m_1\)の直線と平行なので、
\[m_1=\frac{y_1}{x_1}\]
となります。同様に
\[m_2=\frac{y_2}{x_2}\]
が成り立ちますので、まとめると、
\[m_1m_2=\frac{y_1}{x_1}\cdot \frac{y_2}{x_2}=\frac{y_1 y_2}{x_1 x_2} = -1\]
となり証明できました。□
点\(x_1,y_1\)を通り、直線\(ax+by+c=0\)に平行な直線、垂直な直線
数学Ⅱのp.76では、点\(x_1,y_1\)を通り、直線\(ax+by+c=0\)に平行な直線、垂直な直線がそれぞれ、
\[a(x-x_1)+b(y-y_1)=0 \\ b(x-x_1)-a(y-y_1)=0\]
と紹介されていますが、考え方と証明が省かれていますのでここで確認したいと思います。
まず、直線\(ax+by+c=0\)の傾きは、変形すると\(y=-\frac{a}{b}x-\frac{c}{b}\)なので\(-\frac{a}{b}\)となります。つまり、定数aとbによってのみ決まり、それも定数aとbの割合あるいは比によって決まっています。それは、方程式\(ax+by+c=0\)の両辺にどんな同じ実数を掛けても同値であり、方程式を満たす数の組\((x,y)\)は変わらないことからも分かります。
そこで前5章より点\(x_1,y_1\)を通る直線は\(y-y_1=m_1(x-x_1)\)であり、平行な直線であれば傾きは\(m_1=-\frac{a}{b}\)であり、代入して変形すると、\(a(x-x_1)+b(y-y_1)=0\)となります。ただ、傾きが定数aとbによってのみ決まることから、そのままで良い、とも言えます。
他方で、前6章より垂直な直線であれば\(m_1m_2=-1\)なので、\(m_2=\frac{b}{a}\)であり、代入して変形すると、\(-b(x-x_1)+a(y-y_1)=0\)あるいは\(b(x-x_1)-a(y-y_1)=0\)となります。ただ、傾きが定数aとbの比によって決まることから、比も正負も逆と考えれば、aとbを逆にしていずれかにマイナスを付ければ良いとも言えます。
2直線の関係と連立一次方程式の解
数学Ⅱのp.77では2次元座標平面上の2直線の共有点と2直線を表す2つの一次方程式を連立させた解との関係を説明しています。ここでは、復習をかねてその関係の理屈を詳細に点検したいと思います。
まず、一次方程式\(ax+by+c=0\)の解として無数の実数の組\((x,y)\)があるわけです。これを数学Ⅰで学んだ集合として捉えても良いと思います(以下、他の対象についても同じ)。
一方、一つの数直線上のすべての点は実数と一対一対応するのでした。この二つの数直線を直角に交差させた交点(原点)と各数直線上の点の組によって描かれる長方形の原点と反対側の点を取ると、各数直線上の点の組と2次元平面上のすべての点が一対一対応を取ることができると考えるのでした。
そして、各数直線上の点の組は、実数の組\((x,y)\)つまり座標\((x,y)\)と一対一対応を取れるので、結局、2次元平面上のすべての点と座標\((x,y)\)が一対一対応するのでした。
この一対一対応によって、一次方程式\(ax+by+c=0\)の無数の解の組\((x,y)\)は、2次元平面上の無数の点として描かれ、それが直線になるのでした。くわえて、前4章によると、一次方程式\(ax+by+c=0\)と2次元平面上の直線は一対一に対応するのでした(ただし、両辺を0を除いて同じ実数倍したものは同じ方程式とみなします)。
ここまでが復習ですが、さて、この章ではもう一つの一次方程式\(ax’+by’+c=0\)かつそれによって表される2次元平面上の直線を考えるのですが、考え方は先ほどの一次方程式\(ax+by+c=0\)かつ直線とまったく同じです。
それを二つ考えるというだけですが、方程式としては、二つの方程式は連立方程式として計算すると①解を持たない、②一つの解を持つ、③無数の解を持つの3通りがあります。上述より、これらの解の組\((x,y)\)は座標として平面上の点と対応します。①解を持たない場合は、2直線が交点を持たないということであり、②一つの解を持つ場合は、2直線の交点が一つあるということであり、③無数の解を持つ場合は、2直線が一致する場合です。
逆に、2直線の位置関係はその3通りしかなく、二つの方程式の解の場合分けに同様に対応します。2次元平面上のすべての点と座標\((x,y)\)が一対一対応することや、2次元平面上の直線と一次方程式\(ax+by+c=0\)が一対一対応すること、がポイントになっています。
座標を使った三角形の垂心の存在証明
数学Ⅱのp.81では数学Ⅱ第3章「図形と方程式」第1節「点と直線」の仕上げとしてこれらの知識を用いて、座標を使った三角形の垂心の存在証明を行っています。ここでも少しだけ異なった別証明を証明の考え方を含めて詳しく取り上げて、最後にこのページの総仕上げにしたいと思います。
まず、三角形の垂心とは、\(\bigtriangleup\)ABCの三つの頂点から対辺またはそれを延長した直線に垂線を引いたときに、三つの垂線が交わる一点のことを指します。
一般に三つの異なる直線は、3点、2点、1点で交わる場合があります。そのうち、2点の場合にはいずれかの2直線が平行です。三角形の三辺を延長した直線は、互いに一致せず、平行でもないので、これらの垂線も同様に互いに一致せず、平行でもありません。
したがって、三つの垂線は3点又は1点で交わる可能性があるように思われますが、しかし、それが1点で必ず交わるということがポイントになり証明が必要になります。
そこで、数学Ⅱのp.81より引用した次の命題を証明しましょう。
【三角形の垂心の存在証明】
\(\bigtriangleup\)ABCの3つの頂点から、それぞれ対辺またはその延長に下した垂線AL,BM,CNは、1点で交わることを証明せよ。
【証明】
まず、座標で一般的に三角形を扱うために、三角形とは何か、三角形と直線の関係をきちんと整理して考えましょう。
どのように考えるかというと、三角形の特徴を分解して考えます。それは、三角形であれば〇〇の特徴を満たす、というように、数学Ⅰで学んだ必要条件にあたる推論を繰り返せば良いのです。つまり、三角形であるための必要条件を探します。
そして、その見つけ出した特徴(必要条件)をすべて合わせると、三角形(十分条件)になるというところまで、必要条件を探し出します。具体的には、三角形であれば3直線を持つ、三角形であれば各直線は一致しない、三角形であれば各直線は平行ではない、三角形であれば3直線は一点で交わらない、と必要条件を出します。
そうすると、逆に、3直線がそれぞれ一致しなく、平行でなく、かつ、一点で交わらなければ三点で交わりますので、その三点により三角形を作ることができます。したがって、これが三角形を直線で表すための必要十分条件となります。
三角形を直線で表すための必要十分条件が分かれば、このページで二次元座標平面上の直線と一次方程式の一対一対応を繰り返し学んできましたので、三角形を座標で表すための一次方程式の条件を定めることができます。
つまり、3直線に対応する3つの一次方程式
\[a_1x+b_1y+c_1=0 \\ a_2x+b_2y+c_2=0 \\ a_3x+b_3y+c_3=0\]
を考えると、3直線がそれぞれ一致しないとは、\(a,b,c\)がすべて同じではいけないという条件であり、3直線がそれぞれ平行ではないとは、\(a,b\)の比が正負を含めて同じではいけないという条件であり、3直線が一点で交わらないとは、3つの一次方程式のそれぞれ2つを連立した解の組が一つに一致してはいけないという条件です。
一般的に、このような条件の3直線であればその交点は三角形になりますし、逆に、すべての三角形はこのような条件の3直線の3つの交点で表されます。
そこで、この3つの交点を\(\bigtriangleup\)ABCとして、このページの前6章で学んだ垂直条件によって垂線AL,BM,CNを一次方程式で表して、その一次方程式のそれぞれ2つを連立した解の組が一つに一致していることを示せば、垂心が1点に定まるということを証明できることになります。
ただし、多くの場合、このような一般的な形での計算は複雑になります。特に、試験などでは、ここまでのことは前提として頭の中で考えることです。時間がない中ではほとんど考えないことかもしれません。
試験などの場合には、さらに計算が楽になる工夫をすることが重要になります。第一に、上記の一般的な証明では同じ形の異なる大きさの三角形についても同様に証明を行っています。実際には、同じ形で垂心が存在することを示せれば、異なる大きさで証明する必要はありません。中学で学んだ相似という考え方ですね。
そこで、すべての異なる形と異なる大きさの三角形を同一の形によって分類し、各々の形による分類から一つづつ取り出して、その三辺のうちのいずれかの一辺の長さを1に縮小して考えることにしましょう。そうして、その長さ1の1辺をx軸の区間\([0,1]\)に張り付けることとします。
さらに、その辺の反対側の頂点は、どの象限にあっても良いはずですが、第3・4象限にある場合には、第1・2象限に折り返すことにします。そうしても三角形の形は変わらないからです。
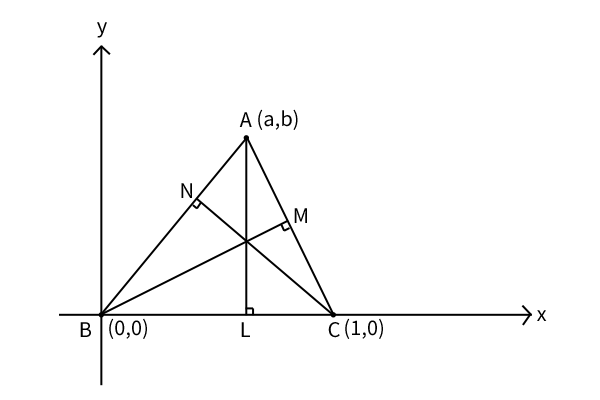
図3:三角形の垂心の存在証明
そうすると、x軸の区間\([0,1]\)を一辺とし第1・2象限\(y > 0\)のいずれかの点を頂点とするすべての三角形を考えれば、すべての異なる形の三角形について考えたことになることが分かります。そこで、上図のように点A(a,b),点B(0,0),点C(1,0)としましょう。ただし、\(b > 0\)です。
ちなみに、試験では「上図のように3点を取れば、すべての三角形について十分な証明を与えられる」などと一言書き、他の問題を解いて時間があればさらに※印などで補足を加えると良いかと思います。
3つの直線AB,BC,CAを表す一次方程式は、前5章のある点を通る直線の方程式を使って、
\[AB: y=\frac{b}{a}x \\ BC: y=0 \\ CA: y = \frac{b}{a-1}(x-1)\]
となります。この3つの一次方程式が、上述した三角形になるための条件を自然に満たしていることも確認しましょう。さらに、各頂点からの垂線AL,BM,CNは、前6章の垂直条件も使って次にようになります。
\[AL: x=a \\ BM: y=-\frac{a-1}{b}x \\ CN: y = -\frac{a}{b}(x-1)\]
では、まず垂線AL,BMの交点を求めると\((a,-\frac{a(a-1)}{b})\)、一方で、垂線BM,CNの交点を求めると\((a,-\frac{a(a-1)}{b})\)と同じ座標、つまり、同じ点であることが分かります。ここで、計算しなくとも垂線CN,ALはどちらも点\((a,-\frac{a(a-1)}{b})\)を通りますので、点\((a,-\frac{a(a-1)}{b})\)は垂線CN,ALの交点でもあることが分かり、垂線CN,ALは一致していないので他の点で交わることはなく、点\((a,-\frac{a(a-1)}{b})\)のみで交わっていることが分かります。
したがって、垂線AL,BM,CNが1点で交わっていることを示せました。つまり、垂線が存在していることを証明できました。□
計算が何倍にも楽になっていることが分かりましたでしょうか。解答は時間を節約してシンプルに書けば良いですが、きちんとした理解が土台になっていることを実感して頂くことが大切です。
それにしても図形だけでは大変な証明が座標を使うとあっという間に済んでしまい、くわえて各三角形に対して正確な垂線や垂心の位置まで簡単に計算できるわけです。点A(a,b)を動かしたときに垂線や垂心の位置がどう変わるのかを少し観察してみてください。デカルトの時代の人々の驚きはいかばかりだったかと察せられます。
著者:L&M個別オンライン教室 瀬端隼也
公開日:2023年1月11日
修正日:-



※このサイトはreCAPTCHAによって保護されています。そのためGoogleのPrivacy PolicyとTerms of Serviceが適用されます。