最大公約数と最小公倍数の計算方法
最大公約数と最小公倍数の計算方法を解説します。まず、基本的な計算方法として、素因数分解を用いた計算方法を復習したいと思います。その上で、最大公約数の計算方法としてのユークリッドの互除法をきちんと解説し、さらに、最大公約数から最小公倍数を求める方法として、最大公約数と最小公倍数の間に成り立つ関係を二つの異なる証明を付けて紹介したいと思います。
【目次】
1.素因数分解を用いた計算方法
2.ユークリッドの互除法
2-1.ユークリッドの互除法の原理
2-2.ユークリッドの互除法
3.最大公約数と最小公倍数の関係
3-1.教科書の方法の詳しい復習
3-2.素因数分解を用いて
4.素因数分解を用いた計算方法の証明
素因数分解を用いた計算方法
教科書(数研出版、高校数学の教科書、以下同じ。詳しくは、高校数学マスター基本方針:参考にする教科書を参照ください)には、最大公約数と最小公倍数の計算方法として、各整数を素因数分解して割り出す方法を解説しています。
つまり、各整数を素因数分解した後に、
具体例:
\[1260\ =\ 2^{2}\cdot 3^{2}\cdot 5^{1}\cdot 7^{1}\cdot 11^{0}\cdot 13^{0}\]
\[990\ =\ 2^{1}\cdot 3^{2}\cdot 5^{1}\cdot 7^{0}\cdot 11^{1}\cdot 13^{0}\]
\[390\ =\ 2^{1}\cdot 3^{1}\cdot 5^{1}\cdot 7^{0}\cdot 11^{0}\cdot 13^{1}\]
最大公約数の場合には、各素因数の指数の最小値を取った積
\[30\ =\ 2^{1}\cdot 3^{1}\cdot 5^{1}\cdot 7^{0}\cdot 11^{0}\cdot 13^{0}\]
を計算すれば良く、
最小公倍数の場合には、各素因数の指数の最大値を取った積
\[180180\ =\ 2^{2}\cdot 3^{2}\cdot 5^{1}\cdot 7^{1}\cdot 11^{1}\cdot 13^{1}\]
を計算すれば良いことになります。
イメージとしては、
底面を各素因数、高さを指数とする立体的なベン図
図1:
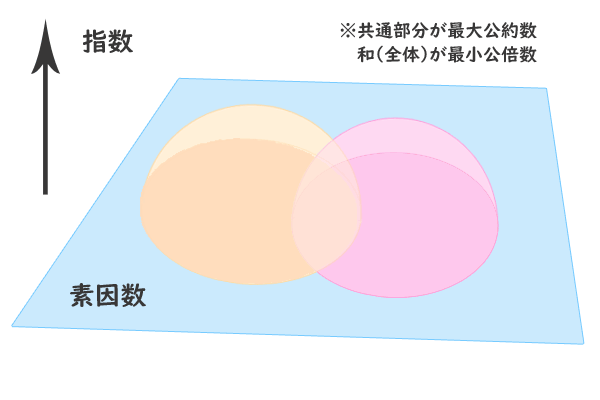
その立体的なベン図を平面に押し付ければ、
\(x\)軸に各素因数、\(y\)軸に指数を並べた平面座標
図2:
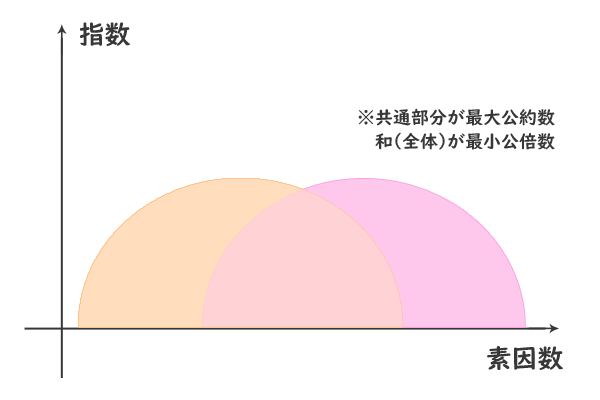
さらに、\(z\)軸に各整数を並べた空間座標
図3:
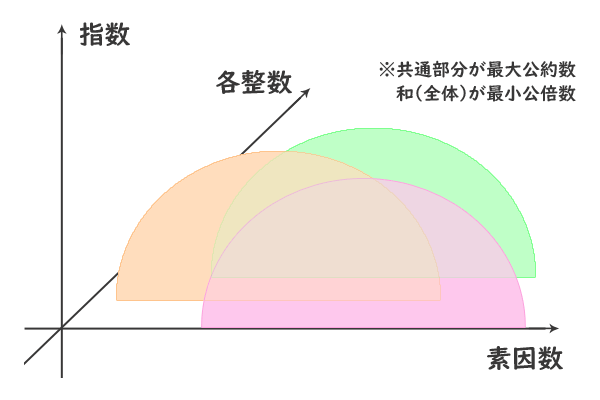
などを考えてみると整理されて分かりやすいのではないかと思います。
以上の説明で正しいことは理解できると思いますが、きちんとした証明を行うと長くなってしまうので、この素因数分解を用いた計算方法が正しいことの証明は、このページの最後に書きたいと思います。
ユークリッドの互除法
最大公約数を計算する効率的な方法と言えば、紀元前のギリシャ時代から変わらずユークリッドの互除法があります。
ユークリッドの互除法の原理
【定理1: ユークリッドの互除法の原理】
整数\(a,b\ (b \neq 0)\)について、\(a\)を割った\(b\)の余りを\(r\)とすると、\(a\)と\(b\)の最大公約数と\(b\)と\(r\)の最大公約数は一致する。
加えて、\(a\)と\(r\)の最大公約数が一致するとは限らないが、\(a\)と\(b\)と\(r\)の最大公約数は一致する。
【証明】
剰余(余り)の一意性(参考:素因数分解の一意性(算術の基本定理)の証明:補題1 剰余(余り)の一意性の証明)より、次の式を満たす整数\(l\)と\(r\ (0 \le r \lt |b|)\)がただ一つ存在します。
\[a= l \cdot b + r \tag{1}\]
つまり、\(l\)は商、\(r\)は余り、ということで、\(a\)を\(b\)で割ると、商と余りの組がただ一つ定まる、と言えます。
\(b\)と\(r\)の最大公約数を\(g_{b,r}\)とします。
数式(1)の右辺において、\(g_{b,r}\)を括りだすことができるので、ある整数\(k\)があって、
\[a=k \cdot g_{b,r}\]
と表すことができます(参考:複数の整数の最大公約数と最小公倍数について:約数と倍数の復習)。
したがって、\(g_{b,r}\)は、\(a\)の約数でもあることが分かりました。
もちろん、\(g_{b,r}\)は\(b\)の約数でもあるので、\(g_{b,r}\)は\(a\)と\(b\)の公約数であることが分かります。
仮に、\(a\)と\(b\)の公約数で\(g_{b,r}\)よりも大きな公約数\(f_{a,b}\)があったとします。
ここで、数式(1)を変形すると、
\[ r = a – l \cdot b \tag{2}\]
となります。
この数式(2)の右辺において、\(f_{a,b}\)を括りだすことができるので、
先ほどと同様に、\(f_{a,b}\)は、\(r\)の約数でもあることが分かりました。
もちろん、\(f_{a,b}\)は\(b\)の約数でもあるので、\(f_{a,b}\)は\(b\)と\(r\)の公約数であることが分かります。
すると、\(b\)と\(r\)の最大公約数\(g_{b,r}\)よりも大きな公約数\(f_{a,b}\)があることになり、矛盾します。
したがって、\(a\)と\(b\)の公約数で\(g_{b,r}\)よりも大きな公約数はないので、\(g_{b,r}\)は\(a\)と\(b\)の最大公約数でもあることが分かりました。
つまり、\(a\)と\(b\)の最大公約数と\(b\)と\(r\)の最大公約数が一致しました。
次は、\(a\)と\(r\)の最大公約数が一致するとは限らない反例を一つ挙げると、
\[(a,b,r)\ =\ (90,21,6)\]
確かに、\(a\)と\(b\)の最大公約数と\(b\)と\(r\)の最大公約数は、\(3\)で一致していますが、\(a\)と\(r\)の最大公約数は\(6\)となり一致しません。
最後に、\(a\)と\(b\)と\(r\)の最大公約数が一致することについては、
複数の整数の集合\(A\)と\(B\)があったときに、\(A\ \cup\ B\)の最大公約数は、\(A\)の最大公約数と\(B\)の最大公約数の最大公約数と一致する(参考:複数の整数の最大公約数と最小公倍数について:系4-1: 最大公約数の最大公約数)という命題が成り立つので、
この命題において、\(A=\{a,b\}\)、\(B=\{b,r\}\)と取れば、\(A\)の最大公約数と\(B\)の最大公約数は共に\(g_{b,r}\)であり、\(g_{b,r}\)と\(g_{b,r}\)の最大公約数はやはり\(g_{b,r}\)なので、\(A\ \cup\ B = \{a,b,r\}\)の最大公約数は\(g_{b,r}\)であることが分かりました。□
ユークリッドの互除法
この【定理1: ユークリッドの互除法の原理】を使って、\(a\)と\(b\)の最大公約数を計算する方法がユークリッドの互除法です。
ポイントは、「\(a\)と\(b\)の最大公約数と\(b\)と\(r\)の最大公約数が一致する」ことと、
「\(0 \le r \lt |b|\)」が成り立つことです。
つまり、二つの整数の組\(a\)と\(b\)から、別の二つの整数の組\(b\)と\(r\)に移しても、両者の最大公約数は変わらず、しかも、必ず、初めの二つの整数\(a\)と\(b\)よりも絶対値の小さな整数\(r\ (0 \le r \lt |b|)\)に移すことができるのです。
この二つの整数の組を移す操作を繰り返し適用すれば、最大公約数は何も変わらずに、二つの整数の組の大きさ(絶対値)だけを小さくしていくことができます。
ちなみに、二つの整数の組\(a\)と\(b\)の正負に関わらず、このことは成り立ちます。
例えば、\(0 \lt a \lt b\)の場合には、余りは\(a\)となるので、1回目の操作で二つの整数の組は変わりませんが、2回目の操作以降ではやはり小さくなっていきます。この場合には、\(a\)と\(b\)を入れ替えて、大きな整数を小さな整数で割る場合と、結果は同じになります。
他に、\(b \lt a \lt 0\)の場合で、1回目の操作で二つの整数の組の絶対値が大きくなってしまうときもありますが、2回目の操作以降ではやはり小さくなっていきます。この場合にも、\(a\)と\(b\)を入れ替えて計算すれば、1回目の操作から小さくなっていきますし、結果は変わりません。
つまり、最も大事なポイントは、「\(0 \le r \lt |b|\)」によって、余りの絶対値が小さくなっていくことです。そして、必ず最後には余りが\(0\)になり、それ以上の操作ができなくなります。
そのときの二つの整数の組を\((c,d)\)として、\(c\)を\(d\)で割った余りが\(0\)とすると、\(c\)と\(d\)の最大公約数は\(d\)になるわけです。
初めの二つの整数の組\(a\)と\(b\)の最大公約数と、最後の二つの整数の組\(c\)と\(d\)の最大公約数は、すべての操作において二つの整数の組の最大公約数が変わらず等しいので、一致します。
したがって、初めの二つの整数の組\(a\)と\(b\)の最大公約数は\(d\)となります。
例えば、分かりづらいけれども重要な具体例として、\(d=1\)の場合には、商\(c\)、余り\(0\ (0 \le 0 \lt 1)\)の組がただ一つ存在して、
\[c=c \cdot 1 + 0\]
を満たします。
したがって、最後の二つの整数の組\(c\)と\(d\)の最大公約数は\(d=1\)となり、初めの二つの整数の組\(a\)と\(b\)の最大公約数も\(1\)となります。
つまり、二つの整数の組\(a\)と\(b\)は互いに素(参考:互いに素な整数に成り立つ重要な定理:「互いに素」の定義の復習)だと分かります。
このユークリッドの互除法を利用して、複数の整数の最大公約数を効率的に求めることもできます。(参考:複数の整数の最大公約数と最小公倍数について:定理5-1: 複数の最大公約数の最大公約数や複数の整数の最大公約数や最小公倍数の求める方法をご覧ください。)
最大公約数と最小公倍数の関係
ユークリッドの互除法によって、最大公約数を求めることができたら、最大公約数と最小公倍数の関係から最小公倍数を計算することもできます。
この方法であれば、上記の「素因数分解を用いた計算方法」よりも効率的に最小公倍数を計算することができます。なぜなら、素因数分解は数が大きくなるほど、計算するのが大変になるからです。
【定理2: 最大公約数と最小公倍数の関係】
教科書には、最大公約数,最小公倍数の性質
として、
2つの自然数\(a,b\)の最大公約数を\(g\)、最小公倍数を\(l\)とする。
\(a=ga^{‘}\)、\(b=gb^{‘}\)であるとすると、次のことが成り立つ。
1.\(a^{‘}\)、\(b^{‘}\)は互いに素である。
2.\(l\ =\ ga^{‘}b^{‘}\)
3.\(ab=gl\) 特に、\(g=1\)のとき\(ab=l\)
と紹介されています。
それでは、以下で二つの証明を確認してみたいと思います。
教科書の方法の詳しい復習
【証明ア:教科書の方法の詳しい復習】
「1.の証明」
仮に、\(a^{‘}\)、\(b^{‘}\)は互いに素でないとすると、\(a^{‘}\)、\(b^{‘}\)には\(1\)より大きな公約数があるので、それを\(c\ (c \gt 1)\)とすると、次の数式を満たす整数\(a^{”},b^{”}\)があります。
\[a^{‘}=a^{”}c, \hspace{20pt} b^{‘}=b^{”}c \]
この式を\(a=ga^{‘}\)、\(b=gb^{‘}\)に代入すると、
\[a=ga^{”}c=(gc)a^{”}, \hspace{20pt} b=gb^{”}c=(gc)b^{”} \]
したがって、\(gc\)が\(a\)と\(b\)の公約数であることが分かりました。
しかし、最大公約数\(g\)よりも大きな公約数\(gc\)があることになり、これは矛盾します。
したがって、\(a^{‘}\)、\(b^{‘}\)は互いに素だと分かりました。
「2.の証明」
最小公倍数\(l\)は、\(a\)と\(b\)の公倍数なので、ある整数\(c\)と\(d\)があって、
\[l\ =\ ca = cga^{‘} = db = dgb^{‘} \tag{1}\]
が成り立ちます。
\(g\)を消去すると、
\[ca^{‘} = db^{‘} \tag{2}\]
が成り立ちます。
\(a^{‘}\)と\(b^{‘}\)は互いに素で、数式(2)の右辺より\(ca^{‘}\)は\(b^{‘}\)の倍数なので、
【互いに素な整数に成り立つ定理】(参考:互いに素な整数に成り立つ重要な定理:定理の証明)より、
\(c\)は\(b^{‘}\)の倍数と分かり、ある整数\(c^{‘}\)があって、
\[c=c^{‘}b^{‘} \tag{3}\]
と表されることが分かります。
数式(1)(3)より、
\[l\ =\ c^{‘}b^{‘}ga^{‘} = c^{‘}(ga^{‘}b^{‘}) \]
より、最小公倍数\(l\)は\(ga^{‘}b^{‘}\)の倍数であることが分かりました。(4)
一方で、\(ga^{‘}b^{‘}\)は、
\[ga^{‘}b^{‘}=b^{‘}(ga^{‘})=b^{‘}a=a^{‘}(gb^{‘})=a^{‘}b\]
より、\(a\)と\(b\)の公倍数です。
ここで、二つの整数の公倍数の集合と最小公倍数の倍数の集合は一致する(参考:複数の整数の最大公約数と最小公倍数について:補題2-2:二つの整数の公倍数と最小公倍数の倍数)ので、
\(ga^{‘}b^{‘}\)は、\(a\)と\(b\)の最小公倍数\(l\)の倍数であることも分かります。(5)
これを踏まえて、仮に、\(ga^{‘}b^{‘}\)と最小公倍数\(l\)が一致しないとすると、
2つの自然数\(a,b\)と最大公約数\(g\)は正の数なので、\(a^{‘}b^{‘}\)も正であり、(5)より\(0 \lt l \lt ga^{‘}b^{‘}\)となります。
しかしながら、これは、先ほど示した事実(4)の最小公倍数\(l\)は\(ga^{‘}b^{‘}\)の倍数であることに矛盾します。
したがって、\(ga^{‘}b^{‘}\)と最小公倍数\(l\)は一致すると分かりました。
「3.の証明」
\[ab=ga^{‘}gb^{‘}=g(ga^{‘}b^{‘})=gl\]
特に、\(g=1\)の場合、つまり、\(a\)と\(b\)が互いに素な場合には、
\[ab=l\]
が成り立ちます。□
次は、素因数分解を用いた証明を行いたいと思います。
上述の「素因数分解を用いた計算方法」で示した具体例や図を参考にしながら考えてもらえると分かりやすいと思います。
素因数分解を用いて
【証明イ:素因数分解を用いて】
「1.の証明」
自然数は一意に素因数分解することができる(参考:素因数分解の一意性(算術の基本定理)の証明:定理 素因数分解の一意性の証明)ので、任意の自然数\(n\)について任意の素因数\(p\)の指数を値に取る関数\(f(n,p)\)を定義することができます。
今、任意の自然数\(k,l\)の最小値を\(min(k,l)\)で表すとすると、任意の素因数\(p\)について、
\[f(g,p)=min(f(a,p),f(b,p))\]
が成り立っています。
したがって、
\[f(a,p)-f(g,p)=0\]
又は
\[f(b,p)-f(g,p)=0\]
が成り立ちます。
一方で、
\[f(a^{‘},p)=f(a,p)-f(g,p),\hspace{20pt}f(b^{‘},p)=f(b,p)-f(g,p)\]
なので、
\[f(a^{‘},p)=0\]
又は
\[f(b^{‘},p)=0\]
が成り立ちます。
したがって、\(a^{‘}\)が素因数\(p\)を持たないか、又は、\(b^{‘}\)が素因数\(p\)を持たないか、が成り立つので、
\(a^{‘}\)と\(b^{‘}\)は、素因数\(p\)を共通しては持たないことになります。
これが任意の素因数\(p\)において成り立つので、\(a^{‘}\)と\(b^{‘}\)が互いに素であることが分かりました。
「2.の証明」
今、任意の自然数\(k,l\)の最大値を\(max(k,l)\)で表すとすると、任意の素因数\(p\)について、
\[f(l,p)=max(f(a,p),f(b,p))\]
が成り立っています。
したがって、\(f(l,p)=f(a,p)\)又は\(f(l,p)=f(b,p)\)が成り立ちます。
そこで、両方の場合を別々に考えると、
\(f(l,p)=max(f(a,p),f(b,p))=f(a,p)\)の場合には、
\(f(l,p)=f(a,p)=f(a^{‘},p)+f(g,p)\)であり、
\(max(f(a,p),f(b,p))=f(a,p)\)より\(min(f(a,p),f(b,p))=f(b,p)=f(g,p)\)なので、
\(f(b^{‘},p)=0\)が成り立ちます。
一方、\(f(l,p)=max(f(a,p),f(b,p))=f(b,p)\)の場合には、
\(f(l,p)=f(b,p)=f(b^{‘},p)+f(g,p)\)であり、
\(max(f(a,p),f(b,p))=f(b,p)\)より\(min(f(a,p),f(b,p))=f(a,p)=f(g,p)\)なので、
\(f(a^{‘},p)=0\)が成り立ちます。
つまり、まとめると、任意の素因数\(p\)について、
\[f(l,p)=f(a^{‘},p)+f(g,p)\ かつ\ f(b^{‘},p)=0 \tag{1}\]
又は、
\[f(l,p)=f(b^{‘},p)+f(g,p)\ かつ\ f(a^{‘},p)=0 \tag{2}\]
が成り立ちます。
数式(1)が成り立つ素因数\(p\)について積をとれば、\(a^{‘}\)が含まれ、\(b^{‘}\)の素因数は一つも含まれません。
同様に、数式(2)が成り立つ素因数\(p\)について積をとれば、\(b^{‘}\)が含まれ、\(a^{‘}\)の素因数は一つも含まれません。
そして、\(g\)の素因数は数式(1)(2)に分かれて存在しています。
したがって、すべての素因数\(p\)について積を取れば、\(l=ga^{‘}b^{‘}\)となることが分かります。
「3.の証明」は先ほどと同じです。□
素因数分解を用いた計算方法の証明
それでは、前述した通りに、最後に「素因数分解を用いた計算方法」の証明を行いたいと思います。
まずは、「素因数分解を用いた計算方法」が正しいことを示すためには、何を証明するべきかをきちんと言葉にします。
【定理3: 素因数分解と最大公約数・最小公倍数】
複数の整数の最大公約数は、各整数を素因数分解して、各素因数の指数の最小値を取った積に等しい。
複数の整数の最小公倍数は、各整数を素因数分解して、各素因数の指数の最大値を取った積に等しい。
【証明】
【定理2: 最大公約数と最小公倍数の関係】で用いた関数\(f,\ max,\ min\)をここでも利用したいと思います。
ただし、先ほど\(max,\ min\)は2つの値のみを取りましたが、以降では複数の値を取れるものとします。
さて、複数の整数全体の集合を\(U\)とします。
まず、最大公約数についてから証明しましょう。
仮に、複数の整数\(U\)のある公約数\(d\)について、そのある素因数\(p\)において、
\[f(d,p) \gt min(\{f(n,p)\ |\ n \in U\})\]
が成り立っているとします。
一方、ある整数\(m \in U\)があって、
\[f(m,p)=min(\{f(n,p)\ |\ n \in U\})\]
が成り立ちます。
したがって、
\[f(d,p) \gt f(m,p) \tag{1}\]
が成り立ちます。
ここで、公約数\(d\)は、\(m\)の約数でもあるので、ある整数\(k\)があって、
\[m=k \cdot d \tag{2}\]
と表されます。
関数\(f\)の定義より、ある整数\(d^{‘},m^{‘}\)があって、
\[d=d^{‘} \cdot p^{f(d,p)}\]
\[m=m^{‘} \cdot p^{f(m,p)}\]
が成立しているので、これを数式(2)に代入して、
\[m^{‘} \cdot p^{f(m,p)}=k \cdot d^{‘} \cdot p^{f(d,p)}\]
\[m^{‘}=k \cdot d^{‘} \cdot p^{f(d,p)-f(m,p)} \tag{3}\]
が成り立ちます。
数式(1)より、\(f(d,p)-f(m,p) \gt 0\)ですが、関数\(f\)の定義より、\(m^{‘}\)は素因数\(p\)を含みません。
したがって、数式(3)は右辺は素因数\(p\)を含むのに、左辺は含まず、矛盾します。
つまり、複数の整数\(U\)のすべての公約数\(d\)について、そのすべての素因数\(p\)において、
\[f(d,p) \le min(\{f(n,p)\ |\ n \in U\})\]
が成り立つと分かりました。
そこで、整数\(g\)を、すべての素因数\(p\)において、\(f(g,p)=min(\{f(n,p)\ |\ n \in U\})\)が成り立つ整数として取れば、たしかにこれは複数の整数\(U\)の公約数でもあり、他のすべての公約数よりも大きいことが分かりました。
次は、最小公倍数について証明します。
仮に、複数の整数\(U\)のある公倍数\(m\)について、そのある素因数\(p\)において、
\[f(m,p) \lt max(\{f(n,p)\ |\ n \in U\})\]
が成り立っているとします。
一方、ある整数\(h \in U\)があって、
\[f(h,p)=max(\{f(n,p)\ |\ n \in U\})\]
が成り立ちます。
したがって、
\[f(m,p) \lt f(h,p) \tag{4}\]
が成り立ちます。
ここで、公倍数\(m\)は、\(h\)の倍数でもあるので、ある整数\(k\)があって、
\[m=k \cdot h \tag{5}\]
と表されます。
関数\(f\)の定義より、ある整数\(m^{‘},h^{‘}\)があって、
\[m=m^{‘} \cdot p^{f(m,p)}\]
\[h=h^{‘} \cdot p^{f(h,p)}\]
が成立しているので、これを数式(5)に代入して、
\[m^{‘} \cdot p^{f(m,p)}=k \cdot h^{‘} \cdot p^{f(h,p)}\]
\[m^{‘}=k \cdot h^{‘} \cdot p^{f(h,p)-f(m,p)} \tag{6}\]
が成り立ちます。
数式(4)より、\(f(h,p)-f(m,p) \gt 0\)ですが、関数\(f\)の定義より、\(m^{‘}\)は素因数\(p\)を含みません。
したがって、数式(6)は右辺は素因数\(p\)を含むのに、左辺は含まず、矛盾します。
つまり、複数の整数\(U\)のすべての公倍数\(h\)について、そのすべての素因数\(p\)において、
\[f(h,p) \ge max(\{f(n,p)\ |\ n \in U\})\]
が成り立つと分かりました。
そこで、整数\(l\)を、すべての素因数\(p\)において、\(f(l,p)=max(\{f(n,p)\ |\ n \in U\})\)が成り立つ整数として取れば、たしかにこれは複数の整数\(U\)の公倍数でもあり、他のすべての公倍数よりも小さいことが分かりました。□
著者:L&M個別オンライン教室 瀬端隼也
公開日:2019年7月30日
修正日:ー



※このサイトはreCAPTCHAによって保護されています。そのためGoogleのPrivacy PolicyとTerms of Serviceが適用されます。