高校生でも分かるように代数学の基本定理の解説と証明
【目次】
0.はじめに
1.代数学の基本定理の解説
2.代数学の基本定理の証明
2―1.実数の大小関係の性質
2―2.前提1:下限の存在、ワイエルシュトラスの定理
2―3.補題:下限を取る複素数の存在
2―3―1.前提2:n次多項式関数の連続性
2―3―2.前提3:集積点の存在定理
2―4.本題の証明の流れ
2―5.本題の解析幾何的証明
はじめに
このページでは、代数学の基本定理を高校生でも分かるように解説、証明したいと思います。高校数学の教科書(数研出版、高校数学の教科書、以下同じ。詳しくは、高校数学マスター基本方針:参考にする教科書を参照ください)では、数学Ⅱ単元「複素数と方程式」の節「高次方程式」で次のように証明なしで紹介されています。
「一般に\(n\)次方程式は、複素数の範囲で、常に\(n\)個の解をもつことが知られている」
この命題は、「代数学の基本定理」という名前が付けられている通り、数学の重要分野である代数学のさらに基本となる定理ですので、きちんと理解をしておくと代数学についての視野が開け、たくさんの応用にもつながります。しかしながら、きちんとした証明は高校数学の範囲ではなかなか難しいので、高校数学の教科書では証明が省かれて紹介のみに留められています。
証明方法は重要な定理なのでたくさんあります。つまり、多くの数学者が関心を持って多種多様な側面からのアプローチを行ってきました。特に、主に18世紀~19世紀頃の数学者の研究対象だったようです。大学の数学課程で最も早く出会う証明方法は、線形代数学の教科書等の付録で出会う、例えば「基礎数学1 線型代数入門 斎藤正彦著」付録Ⅰp.230(参考文献一覧はページ下部)に掲載されている方法でしょうか。定理についての理解が深まり、多くの証明方法と出会い始めるのは、微分積分学を学んで解析学の複素解析学を学び始めてからだと思います。
以下では、厳密な理解に基づく証明には、三点さらなる詰めの勉強が必要ですが、できる限り高校生でも理解ができるように代数学の基本定理を解説し、またその証明を工夫して考えてみました。それでは早速、解説から入りたいと思います。
代数学の基本定理の解説
代数学の基本定理については、恒等式の次数と係数、根の個数の条件の証明:発展:線形代数や代数学の基本定理との関連でも書きましたが、代数学の基本定理とは、「複素係数(したがって実数係数も)の\(n \geq 1\) 次方程式は複素根を持つ」という命題で、これに剰余の定理(あるいは因数定理)を繰り返し用いれば、「複素係数の\(n \geq 1\) 次方程式は複素根を重複を含めて丁度\(n\)個持つ」という命題が簡単に導かれるので、使い勝手の良い後者を代数学の基本定理として言及する場合もあります。
代数学の基本定理の歴史的な経緯については、教科書のコラムに合わせて複素数の積が0ならば、いずれかは0である代数的証明:おまけ:教科書の各章冒頭コラムについてにて、\(n\)次方程式の解の存在や解の公式の存在が論点となり代数学の発展を促してきたという数学史に触れました。興味のある方は、こちらの代数学の基本定理に関する辻 雄先生のpdfを読むと、より詳しく教科書のコラムに記載されている辺りの歴史的な背景も分かると思います。
つまり、時の天才たちが代数学の基本定理に関する証明を行ったこと、ガウスの証明が当時においては完全な厳密性を持った初めての証明であったこと、アーベルが5次以上の方程式の解の公式の存在を初めて否定したこと、ガロアが少し遅れて群論を発見してより洗練された一般的な理論でその存在を否定的に示したこと、5次以上の方程式について解の公式(係数から加減乗除とべき根により解を導く操作)はなくとも解の存在を具体的な数値としてある数列の極限を用いて求めることにワイエルシュトラスが成功したこと、などです。
辻先生のpdfを読んで、私が改めて興味深いと思った2点は、まず、時の天才たちが行った代数学の基本定理に関する証明は、その当時では、厳密性を欠いていたけれども後の研究成果を適用すれば証明は成立していたという点です。これはどの時代においてもよくある現象であると感じます。つまり、天才たちはある命題について自明のこととして真であることを理解するのですが、論理的には厳密性を欠く、あるいは普通の人には飛躍となってしまい、後世に訂正あるいは補強が必要となるという数学史的な経緯です。2点目は、解を具体的に示すことに成功したのがワイエルシュトラスだったということです。ワイエルシュトラスは、後でワイエルシュトラスの定理をご紹介しますが、解析学に多大な功績を残した数学者です。厳密な理論と共に具体的で精巧な手法の開発もできるワイエルシュトラスの数学者としての凄みのようなものを感じました。
上記の辻雄先生のpdfに紹介・解説された証明をきちんと理解するには大学数学の知識が必要だと思います。このページでは、辻先生のpdfの「D’Alembert, Argand, Cauchyの方法」と「幾何的証明」の解法を主に参考にして、できる限り高校生でも理解できるように証明を工夫して考えてみました。以下に証明を示しますが、解説程度にお読みいただき誤り等ありましたらご指摘いただければ幸いです。
代数学の基本定理の証明
【代数学の基本定理】
「複素係数の\(n \geq 1\) 次方程式は複素根を持つ」
【証明】
まず、実数の大小関係についての性質から説明をしたいと思います。
実数の大小関係の性質
ある実数の集合Sについて、集合Sに属するすべての数についてそのすべての数以下の数Mがあったときに、Mを下界と言います。Mとなる数が一つでもあればそのM以下の数はすべてやはり下界ですが、下界の中でも最大の数が仮にあれば、その数を最大下界あるいは下限と言います。
なぜ下限と呼ぶのかというと、下限は下界であることから集合Sに属するすべての数は下限以上であり、かつ、集合Sの下方の区切りになっているからです。というのは、仮に下限よりも少しでも大きな数M’があったとすると、M’は下界の中でも最大の数である下限よりも大きいので、下界ではなく、下界ではないということは、つまり、集合Sに属する少なくとも一つの数についてM’よりも小さくなる数があるということになり、M’は下方の区切りとしての役割を果たせないからです。逆に、下限は下界の最大値でもあり、集合Sとその下界の区切り、つまり、集合Sの下方の区切りとしての役割を果たしているわけです。
ちなみに、下限は下界ですが、集合Sに含まれている場合もあれば、含まれていない場合もあります。含まれている場合には集合Sの最小値であり、含まれていない場合には集合Sの数が無限に下限に近付いていくことになります。なぜなら、含まれていない場合に集合Sの数が無限に下限に近付いていかないとすると、いずれかに下限よりも大きな値として下界を取ることができてしまい、下限が最大の下界であることと矛盾してしまうからです。
前提1:下限の存在、ワイエルシュトラスの定理
さて、このページの冒頭で「厳密な理解に基づく証明には、三点さらなる詰めの勉強が必要です」と言ったのは、まずその一点については、上記では「仮に」とした下限の存在について、下界が存在すれば下限も存在するという命題を証明抜きに利用したいと思うからです。
下界が存在するということは、集合Sは下方に無限に小さくなることがないということを意味します。そのような場合に、「下界の最大数がある」、あるいは、「下界かつそれよりも大きな数は集合Sに属する少なくとも一つの数よりも大きくなってしまう、そのような数がある」、という主張を証明抜きに利用したいわけです。この主張をワイエルシュトラスの定理と言います。改めてワイエルシュトラスの定理を明記すると、
ワイエルシュトラスの定理:
実数の集合Sに下界があれば、Sの下限が存在する。
たしかに、集合Sが無限に負に発散しないのであれば、どこかで最小値を取るか、最小値のようにどこまでも近づいていく値があるかの二通りしかなく、どちらにせよ区切りとなる数はあるだろうと、直感的にも自明なことのように感じるかもしれません。したがって、これを前提としても良いのですが、厳密に正しいことを理解するためには実数の連続性を明確化することが必要になります。
以上の内容は「解析概論 高木貞治著」を引用、参考に記述させて頂きました。より詳しく「詰めの勉強」をされたい方は、当該書籍を参考にしてください。
補題:下限を取る複素数の存在
次に、複素係数の\(n\)次多項式関数を以下のようにおいて、
\[f(z)=a_n z^n+a_{n-1} z^{n-1}+ \cdots + a_1 z + a_0 \]
ただし、\(a_n \neq 0\)とします。そしてまず、ワイエルシュトラスの定理を用いて下記の補題を証明したいと思います。
【補題:下限を取る複素数の存在】
すべての複素数\(z\)について、
\[|f(z)|\geq |f(c)|\]
を満たす複素数\(c\)が存在する。
\(|f(z)|\)の取る値は、複素数の絶対値なので実数集合です。これを集合Sとします。\(|f(z)| \geq 0\)より\(0\)は集合Sの下界となります。ワイエルシュトラスの定理より、集合Sは下限を持つことが分かります。それを下限Mとします。\(M’ > M\)を満たす任意の数M’について、Mは下限なので\(M’ > |f(z)| \geq M\)を満たす\(z\)が存在します。
ここで\(|f(z)| = M\)を満たす\(z\)があれば、これが\(c\)となります。
一方で、仮に\(|f(z)| = M\)を満たす\(z\)がない場合には、M’をMに限りなく近づけていくことで、\(|f(z_i)| > |f(z_{i+1})| > M\)を満たす点列\(\{z_i\}\)を取ることができます。なぜなら、次々にM’を\(|f(z_i)|\)よりもMに近い値に取れば良いからです。
前提2:\(n\)次多項式関数の連続性
ここで、二点目の「詰めの勉強」が必要な個所なのですが、\(f(z)\)を実係数の実数を定義域として考えた場合には高校数学でも\(n\)次多項式関数はすべての実数において連続であることを学ぶと思います。つまり、任意の実数\(z_0\)で、
\[\lim_{z \to z_0}f(z)=f(z_0)\]
が成り立ちます。このことは、複素係数の複素数を定義域とする\(n\)次多項式関数でも同様に成り立ちます。また、その絶対値\(|f(z)|\)も連続となります。これらのことを証明抜きに利用したいと思います。より詳しく「詰めの勉強」をされたい方は、「解析概論 高木貞治著」p.25や「複素関数入門 R.V.チャーチル/J.W.ブラウン著 中野實訳」p.30,31をご覧ください。
前提3:集積点の存在定理
さらに三点目の「詰めの勉強」が必要な個所なのですが、複素平面を思い浮かべて頂き、点列\(\{z_i\}\)について、ある点Aの周りのどれほど近いところにも点列\(\{z_i\}\)の点が無数にある、そのようなある点Aが必ず存在することを主張したいのです。この点Aのように、ある集合や点列に属する点がどれほど近いところにも無数にある、そのような点のことを集積点と呼びます。そこで、次の定理をこのページでは前提としたいと思います。
集積点の存在定理:
有界なる無数の点の集合に関して、集積点が必ず存在する。
上記は「解析概論 高木貞治著」p.15より引用させて頂きました。より詳しく「詰めの勉強」をされたい方は、当該書籍を参考にしてください。ちなみに、これもワイエルシュトラスの定理と言うそうです。いかにワイエルシュトラスがこの分野で活躍したかが分かり感嘆させられます。
この定理において「有界なる」という条件は、複素平面において\(|z|\)が無限に発散しないということです。つまり、ある半径\(r\)の円にすべての集合や点列を含むことができる、ということと同値になります。それでは、点列\(\{z_i\}\)は有界でしょうか。点列\(\{z_i\}\)とは、\(|f(z_i)| > |f(z_{i+1})| > M\)を満たす点でしたが、\(f(z)\)を次のように変形して\(|z|\)を無限に発散させると、
\[f(z)=z^n(a_n +a_{n-1} \frac{1}{z}+ \cdots + a_1 \frac{1}{z^{n-1}} + a_0 \frac{1}{z^n})\]
括弧内の各項は定数\(a_n\)以外は\(0\)に収束することが分かります。そうすると、\(a_n \neq 0\)なので括弧内は\(0\)以外の複素数に収束することが分かります。そして、\(|z^n|\)は無限に発散するので結局、\(|f(z)|\)も無限に発散することが分かりました。したがって、点列\(\{z_i\}\)が有界ではなく、すなわち\(|z_i|\)が無限に発散すると仮定すると、\(|f(z_i)|\)も無限に発散するのですが、これは点Mに近づいていくという条件\(|f(z_i)| > |f(z_{i+1})| > M\)に矛盾します。したがって、点列\(\{z_i\}\)は有界であることが分かりました。
したがって、集積点の存在定理を用いることができ、点列\(\{z_i\}\)には集積点があることが分かり、これを集積点\(c’\)としましょう。集積点\(c’\)の周りの無数の点を改めてある集合\(\{z’_i\}\)とすると、これは点列\(\{z_i\}\)の部分集合なので、やはり条件\(|f(z’_i)| > |f(z’_{i+1})| > M\)を満たす点列に並び直すことが出来ます。つまり、点列\(\{z’_i\}\)が集積点\(c’\)に限りなく近づいていくときに、\(|f(z’_i)|\)も限りなく実数Mに近づいていくことになります。
そうすると、先ほど述べた\(|f(z)|\)の連続性から下記の二つ目の等号が成り立ち、
\[M=\lim_{z’_i \to c’}|f(z’_i)|=|f(c’)|\]
となり、\(M=|f(c’)|\)であり、この集積点\(c’\)の存在は、「仮に\(|f(z)| = M\)を満たす\(z\)がない場合」とした仮定に反するので、
\[|f(z)|\geq M=|f(c)|\]
を満たす複素数\(c\)が存在する場合しかないことが言えました。
本題の証明の流れ
これで補題の証明ができましたので、本題へと入っていきたいと思います。本題を復習すると、【代数学の基本定理】「複素係数の\(n \geq 1\) 次方程式は複素根を持つ」とは、
\[f(z)=a_n z^n+a_{n-1} z^{n-1}+ \cdots + a_1 z + a_0 = 0 \]
を満たす\(z\)が複素数に存在するということです。このことと【補題】の結果を複素平面で考えると、以下の問題が生じることが分かります。下図のように\(z\)を関数\(f\)で飛ばした値域である\(f(z)\)についての複素平面を考えると、
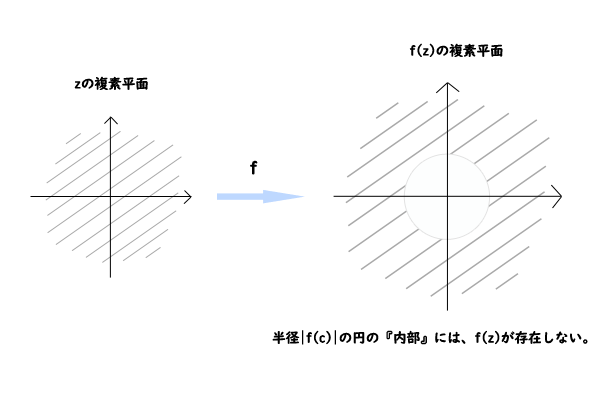
図1:\(f(z)\)についての複素平面
補題より\(|f(z)|\geq |f(c)|\)なので、長さ\(|f(c)|\)を半径とする円Oの内部には\(f(z)\)は存在しないことが分かります。そうすると、\(|f(c)| > 0\)の場合には、\(|f(z)|\geq |f(c)| > 0\)、つまり、\(|f(z)| > 0\)であり、\(f(z) = 0\)を満たす複素数\(z\)は存在しないことになります。そうすると、【代数学の基本定理】は成立しないという結論になってしまうわけです。
そこで、\(|f(c)| > 0\)の場合には矛盾が生じることを示せれば、\(|f(c)| > 0\)又は\(|f(c)| = 0\)しかないので、結論として\(|f(c)| = 0\)が成り立つことになり、すなわち、\(f(c) = 0\)が成り立ち\(c\)が複素根として存在することを示せることになります。
したがって、これから\(|f(c)| > 0\)の場合に矛盾が生じることを示したいと思います。おおまかに言うと、仮に\(|f(c)| > 0\)であるとすると、補題より長さ\(|f(c)|\)を半径とする円の内部には\(f(z)\)は存在しないはずなのに、\(n\) 次多項式関数の性質から\(f(z)\)が存在してしまうことを示したいと思います。
それでは、\(|f(c)| > 0\)を仮定して議論を進めたいと思います。
本題の解析幾何的証明
そもそも\(f(z)\)とは、\(z\)についての複素平面から\(f(z)\)についての複素平面への関数と捉えることが出来ます。そこで、考察を簡明にするために、\(z\)についての複素平面において\(c\)が原点となるように、\(f(z)\)についての複素平面において\(f(c)\)が原点となるように、\(f(z)\)を平行移動させた関数\(h(z)\)へ以下のように置き直すことにします。
まず、\(z\)についての複素平面において\(c\)が原点となるように\(g(z)\)を次のように置きます。
\[g(z)=f(z+c)\]
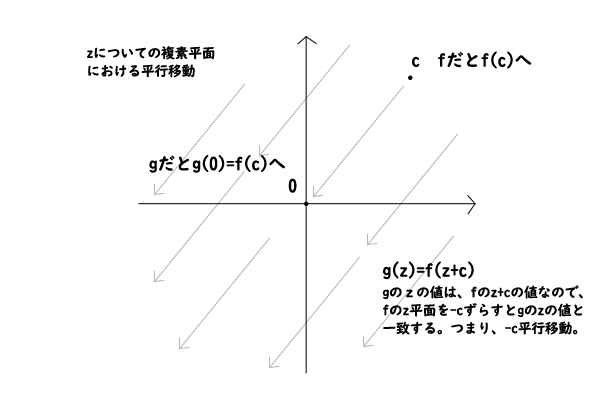
図2:\(z\)についての複素平面における平行移動
さらに、\(f(z)\)についての複素平面において\(f(c)\)が原点となるように\(h(z)\)を次のように置きます。
\[h(z)=g(z)-g(0)=f(z+c)-f(0+c)\]
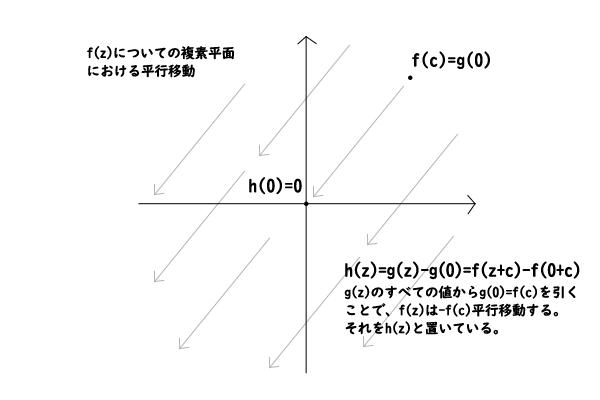
図3:\(f(z)\)についての複素平面における平行移動
\(c\)も\(f(c)\)も定数ですので、計算すれば\(h(z)\)は係数と定数項は異なりますが、やはり\(n\)次多項式関数であることが分かります。加えて、\(h(z)\)は\(f(z)\)を定義域と値域の複素平面において平行移動させただけの関数なので、\(f(z)\)の円Oに対応する\(h(z)\)における円O’の内部に\(h(z)\)が入るような\(z\)が存在すれば、円Oの内部に\(f(z)\)が入るような\(z\)が存在するということが言えます。
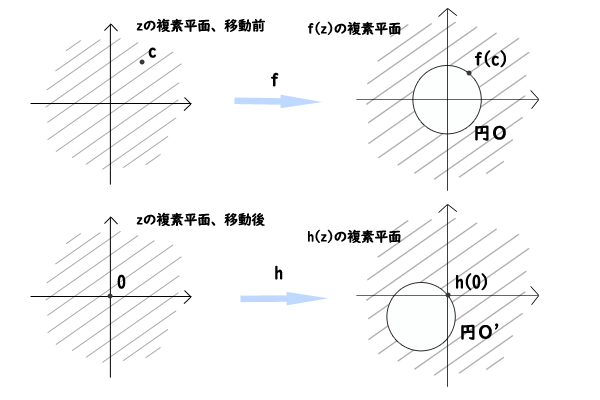
図4:\(f(z)\)と\(h(z)\)の対応関係
そこで、\(h(z)\)を、
\[h(z)=b_n z^n+b_{n-1} z^{n-1}+ \cdots + b_1 z + b_0 \]
とし、ただし、\(b_n = a_n\)です。さらに、\(h(0)=f(0+c)-f(0+c)=0\)より、\(b_0=0\)となりますので、
\[h(z)=b_n z^n+b_{n-1} z^{n-1}+ \cdots + b_1 z \]
となります。
まず、\(z\)の絶対値を\(r > 0\)、偏角を\(\theta\)としましょう。ここで、定義域の複素平面において\(z\)を原点の周りに
\(r\)を十分に小さな値で固定して一周した場合に、値域の複素平面において\(h(z)\)が原点の周りを十分に小さな値で一周するとすれば、下図のように必ず円O’の内部に\(h(z)\)が入るような\(z\)が存在することになります。
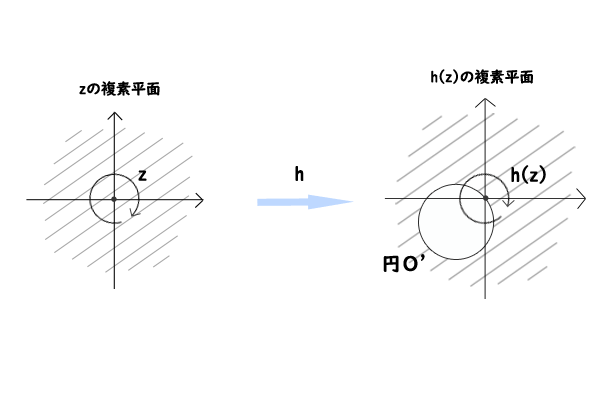
図5:解析幾何的証明
したがって、この事実を証明したいと思います。\(h(z)\)を\(r > 0\)を使って変形すると、
\[h(z)= r(b_n \frac{z^n}{r}+b_{n-1} \frac{z^{n-1}}{r}+ \cdots + b_1 \frac{z}{r}) \]
今、とりあえず\(b_1 \neq 0\)の場合を考えるとすると、\(r\)を限りなく\(0\)へと小さくしていくと、上式の括弧の中の\(b_1 \frac{z}{r}\)の項は、\(b_1(cos\theta + i sin\theta)\)となり\(r\)に対して定数であり、その他の項は\(r\)のべきが少なくとも一つ以上残るので\(0\)に限りなく近づいていきます。括弧の外に\(r\)がありますので、\(h(z)\)の全体も\(0\)に限りなく近づいていくことが分かります。
そこで、\(r\)を十分に小さくとれば、図6のように任意の\(\theta\)について、
\[|b_1(cos\theta + i sin\theta)| > \sum_{k=2}^{n} |b_k \frac{z^k}{r}|\]
が成り立ち、各項の複素数がどのような偏角を取ったとしても\(\theta\)方向について原点から十分な距離が空くことが分かります。と同時に\(2r|b_1(cos\theta + i sin\theta)|\)よりも原点から離れることがないことも分かります。
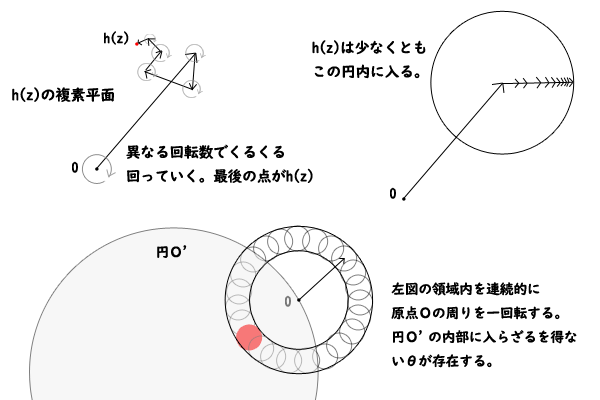
図6:\(0\)の周辺のベクトル
したがって、\(z\)の\(r\)を十分に小さくとって\(\theta\)を一回転させれば、\(h(z)\)の全体は\(0\)に十分に近づいた上で\(0\)の周りを連続的に一回転することが分かります(ただし、どのような形の一回転かは考えていませんし本証明には必要ないでしょう)。そうすると、必ず円O’の内部に\(h(z)\)が入ることになるので、そのような\(z\)が存在することが分かりました。
ここまで、\(b_1 \neq 0\)の場合を考えてきましたが、以上のことは\(b_i \neq 0\)を満たす最小の次数の項について同様に考えれば成り立ちます。違いとしては括り出す\(r\)のべき数が変わることと、一回転より多く回転することくらいかと思います。
最後に議論を遡れば、円O’の内部に\(h(z)\)が存在することが言えたので、\(|f(c)|\)を半径とする円Oの内部に\(f(z)\)が存在することが言え、\(|f(c)| > 0\)の場合に矛盾が生じることを示せました。すなわち、\(f(c) = 0\)が成り立ち\(c\)が複素根として存在することを示せました。□
以上の証明を要約すると、「\(n\)次多項式関数の絶対値には実数の性質から下限がある。下限の十分に小さな周辺について\(n\)次多項式関数の極端に大きな付近の発散する性質と相容れないことから定義域は有界に取れ、それと\(n\)次多項式関数の連続性から下限を取る値がある。\(n\)次多項式関数の極端に小さな付近の幾何的な性質から下限は\(0\)でなければならない。したがって、複素根がある。」となります。つまり、実数の持つ性質、\(n\)次多項式関数の極大、極小における性質を上手に使っていることがポイントだと思います。
参考文献:
[1]「基礎数学1 線型代数入門」 斎藤正彦 東京大学出版会 第49刷
[2]「定本 解析概論」 高木貞治 岩波書店 第7刷
[3]「複素関数入門〔原書第4版〕 Complex Variables and Applications」 R.V.チャーチル/J.W.ブラウン 中野實訳 サイエンティスト社 第12刷
[4]「代数学の基本定理」 辻雄 東京大学大学院数理科学研究科グローバルCOEプログラム『数学新展開の研究教育拠点』2010年度公開講座 『複素数の話』予稿集 2010年11月6日 https://www.ms.u-tokyo.ac.jp/activity/documents/tsuji.pdf 2021年7月15日アクセス可
公開日:2021年7月16日
修正日:-





※このサイトはreCAPTCHAによって保護されています。そのためGoogleのPrivacy PolicyとTerms of Serviceが適用されます。