高校生でも分かるように微分積分学の基本定理の解説と証明
【目次】
0.はじめに
1.微分積分学の基本定理の解説
2.微分積分学の基本定理の証明
2―1.原始関数の定義
2―2.積分→微分(微分積分学の第一基本定理)の証明
2―3.微分→積分(微分積分学の第二基本定理)の証明
2―3―1.定積分の公式(微分積分学の基本公式)
2―4.微分→積分(微分積分学の第二基本定理)の別証明
3.まとめ
はじめに
今回は、微分積分学の基本定理の解説と証明をしたいと思います。微分積分学の基本定理とは、簡単に言うと微分と積分が逆演算となっていること、つまり、関数\(f(x)\)を積分して微分すると\(f(x)\)に、微分して積分すると\(f(x)+C\)に戻るという定理です。
通常、連続関数の場合は、前者は微分積分学の第一定理とも呼ばれ、関数\(f(x)\)と\(x\)軸に囲まれた区間の面積の関数\(F(x)\)を用いて\(F'(x)=f(x)\)と表され、後者は微分積分学の第二定理とも呼ばれ、関数\(f(x)\)の一つの原始関数\(F(x)\)ですべての原始関数が\(F(x)+C\)と定数の違いのみで表されることを指します。また、この二つの定理から次の微分積分学の基本公式が導かれ、
\[\displaystyle \int_a^{b} f(x)dx = F(b)-F(a)\]
関数\(f(x)\)と\(x\)軸に囲まれた区間\((a,b)\)の面積を計算することができます。
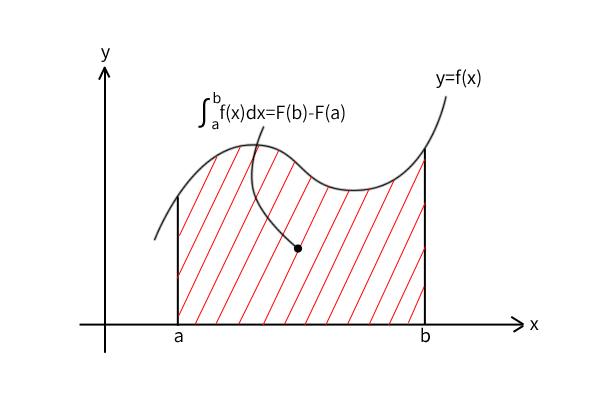
図1:微分積分学の基本公式
このページでは、上記のように微分と積分が逆演算になっていること、ニュートンやライプニッツ以前には計算が難しかった様々な図形の面積や体積の計算が簡単にできるようになった、その理由を微分積分を初めて学ぶ方でもきちんと理解できるように証明付きで解説したいと思います。
微分積分学の基本定理の解説
高校数学の教科書(詳しくは、高校数学マスター基本方針:参考にする教科書を参照ください。以下同じ。)の数学Ⅱ第6章「微分法と積分法」第3節「積分法」では、微分積分学の基本定理をコラムで説明し、実際上は本文でも同様の内容を扱っています。ただ、おそらく読者層と紙数の問題により、微分と積分が逆演算であることへの言明はないので、その事実や重要性へのきちんとした理解は得にくいのではないかと思います。
微分と積分が逆演算であることを理解すると、微分積分学の基本公式を導くことができるだけではなく、例えば、教科書の数学Ⅲ第7章「積分法」で学ぶ置換積分法や部分積分法が微分法の法則の逆演算として証明されていることなど、微分と積分が相互補完的に互いの法則を活用して発展してきたことを知ることができます。
そもそも、歴史を振り返ると、ニュートンとライプニッツが微分積分学の基本定理を発見しましたが、その発見に至る歴史的な過程は決して容易なものではありませんでした。最も重要な契機は、別の記事「図形と方程式とデカルト、高校数学と科学の基礎について」でも解説しましたが、デカルトによる座標の発見、つまり、代数学と幾何学の融合がその発見の土台となりました。
というのは、それまでも古代ギリシャ以来、幾何学において接線の傾きや個別の図形の面積や体積の求積法は長く研究されてきました。つまり、現在でも教科書に掲載されているような接線や面積を極限を用いて求める方法(例えば短冊を埋め尽くしていく方法)は知られていたということです。しかし、それらの記述は数式を用いたものでもなければ、座標上におかれた図形についてでもありませんでした。傾きと面積については、それらが関係していることすら想像しておらず、まったく独立した研究対象でした。
それは、ただ図形を紙面上に描いているだけでは、たしかに気付く糸口がないのではないかと現代でも容易に想像できるのではないでしょうか。詳しくは後述するように、やはり、座標上で曲線を描いてみて初めて、その曲線の関数\(f(x)\)と\(x\)軸に囲まれた区間の面積に意識が行き、そして曲線を表す数式(関数\(f(x)\))との関係を調べてみようという気になるからです。
そこまで来てさらに、その面積を関数\(F(x)\)として表わしたうえで下図のように別の座標に曲線として描き直し、その曲線の傾きを微分によって求めてみて初めて、その傾きを表す数量が元の座標では\(f(x)\)を表す数量でもある、つまり、「曲線\(F(x)\)の傾き」=「面積\(F(x)\)の切り口の長さ」=「曲線\(f(x)\)への\(x\)軸からの長さ」、ということに気付くのだと思います。
そして、それは言い換えると、曲線\(f(x)\)に囲まれた面積\(F(x)\)を求めて曲線\(F(x)\)の傾き\(f(x)\)を求めることであり、面積と傾きが逆向きの関係であること、つまり、面積を求める積分と傾きを求める微分が逆演算であり元の関数\(f(x)\)に戻ることを示す微分積分学の第一基本定理に近づいていくのです。
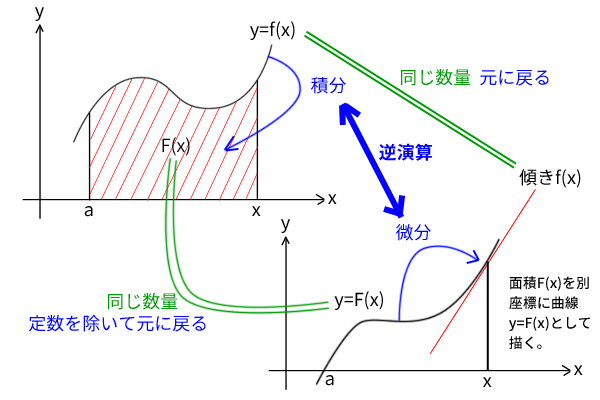
図2:微分積分学の基本定理
理論上は、まずデカルトの座標発見の後に、それまで様々な図形について個別の計算法で求めていた曲線の傾きは、その曲線を表す関数\(f(x)\)を微分すれば求められるようになります。さらに、上述の微分積分学の基本定理の発見により、同様にそれまで微分とはまったく関係なく様々な図形について個別の計算法で求めていた曲線に囲まれた面積は、その曲線を表す関数\(f(x)\)に対して「微分をして関数\(f(x)\)になる関数\(F(x)\)」を見つけるだけで計算ができるようになりました。つまり、大量の曲線の傾きと面積が、ほぼ数式上の計算である微分のみであっという間に算出できるようになったのです。
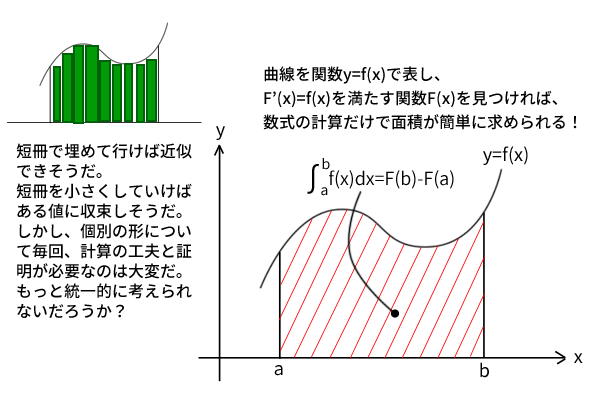
図3:微分積分学の基本定理と基本公式の驚き
当時の人々にとっては驚異の定理であり、現在の私たちからしても様々に複雑な形を示す曲線の面積がなぜその数量でよいのか?(数式を微分したり代入計算するだけで、、)、つまり、微分積分学の基本定理を理解していなければ不思議で仕方がない驚きがそこにはあると思います。
くわえて、前述した記事「図形と方程式とデカルト、高校数学と科学の基礎について」でも解説しましたが、デカルトは一般に科学的な対象に表れる様々な数量を数式で幾何学的に表現するための理論として座標を考案したので、その通りに、単に図形だけではなく、広く数量で表すことができるどんな対象でも、たとえ本当は目には見えないようなエネルギーや重力や細胞増殖や貨幣価値でも何でも、図形(主に曲線)として表わすことができ、その傾きや面積として微分積分で求めた数量を分かりやすく認識することができるようになったのです。
ここまでで微分積分学の基本定理の重要性を少し感じて頂けたでしょうか。それだけではなくこのような歴史経過を見ると、微分積分学の発展は座標上で考えることによってもたらされた側面が大きいと分かると思います。したがって、初めて微分積分学を学ぶ場合も数式だけの極限操作や速度のように「目には見えない(認識しにくい)」科学事例だけを扱うのではなく、座標を駆使して幾何学的・視覚的な理解を伴う学習をすることがポイントではないかと思います。
くわえて、上記あるいは上記記事でも説明していますが、座標を駆使するためには、座標上で扱う変数は自在に取り直すことができるという理解が必要であり、これによって関数と幾何学的対象を繋げたり切り離したりすることができます。この座標を自在に用いることができるようになることも理解を深めるためのポイントではないかと思います。この点は、後述の証明を読めば理解いただけると思います。
それでは、以上のような先人の驚きを追体験して頂けるように、次章からは微分積分学の基本定理を初めて学ぶ方でも分かりやすいように座標上の図形をきちんと明示したうえで、また、厳密すぎて理解できないということがないよう、かといって疑問の余地のできるだけ少ない論法を用いて解説と証明を行います。
微分積分学の基本定理の証明
まず、微分積分学の基本定理による最終目標をきちんと確認しておきましょう。
微分積分学の基本定理は、簡単に言うと関数\(f(x)\)を積分して微分すると\(f(x)\)に、微分して積分すると\(f(x)+C\)に戻るという定理でした。そして、この定理から冒頭の微分積分学の基本公式が求められ、「微分をすると\(f(x)\)になる関数\(F(x)\)」を一つでも見つければ微分積分学の基本公式から関数\(f(x)\)と\(x\)軸に囲まれた区間\((a,b)\)の面積を計算することができるのでした。
この「微分をすると\(f(x)\)になる関数\(F(x)\)を一つでも見つければ、関数\(f(x)\)と\(x\)軸に囲まれた区間\((a,b)\)の面積を計算することができる」ことが微分積分学の基本定理と基本公式の革新的な点で、様々な図形の面積の計算を驚くほど簡便にしたのでした。
原始関数の定義
したがって、「微分をすると\(f(x)\)になる関数\(F(x)\)」は面積の計算のためには重要な関数になるわけです。そこで、この関数\(F(x)\)を原始関数と呼びます。つまり、原始関数の定義は、「微分をすると\(f(x)\)になる関数」です。
ただし、このページの現時点では、原始関数が関数\(f(x)\)と\(x\)軸に囲まれた区間\((a,b)\)の面積に関係する関数であるかはまだ何も分かっていません。一つづつ証明をしていきましょう。
積分→微分(微分積分学の第一基本定理)の証明
このページで扱う関数は、簡単のために2変数の連続関数に限りましょう。それでも高校数学で扱う関数のほとんどは連続関数に含まれています。\(y=x^2\)などのn次多項式の関数も指数関数や対数関数も連続関数です。連続関数とは、平面座標上で関数が表す曲線が切れたりせずにいずれの点でも繋がっていることを意味します。
下図のように連続関数\(f(x)\)を平面座標上に曲線として描き、定数\(x=a\)から変数\(x=t\)までの区間\((a,t)\)で囲まれた図形の面積を考えます。全体が連続した線に囲まれていますので、直観的に面積がいずれかの実数で決定できるという前提は受け入れることにしたいと思います。そうすると、その面積は変数\(t\)が決まると同時に決定するはずなので、変数\(t\)の関数として表わすことができ、これを関数\(G(t)\)としましょう。
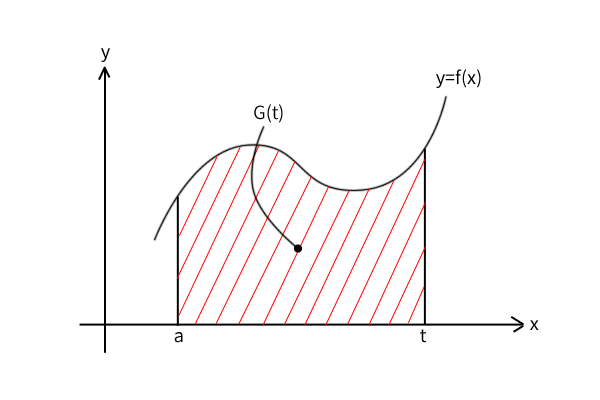
図4:曲線\(f(x)\)と\(x\)軸に囲まれた区間\((a,t)\)の面積の関数\(G(t)\)
通常、高校数学の範囲では、積分するとは原始関数を求めること、あるいは、求めた原始関数より面積\(G(t=b)\)を計算することを意味しますが、ここでは関数\(G(t)\)を求めること、あるいは、関数\(f(x)\)と\(x\)軸に囲まれた区間\((a,t)\)の面積を求めることを指すことにしましょう。
そうすると、微分積分学の第一基本定理は、関数\(f(x)\)を積分して微分すると\(f(x)\)に戻るという定理でしたので、正確には次のことを意味します。
【微分積分学の第一基本定理】
関数\(f(x)\)を積分した関数\(G(x)\)を微分すると関数\(f(x)\)に戻る、つまり、
\[G'(x)=f(x)\]
が成り立つ。
【証明】
下図のように点\(x=t\)よりほんの少し\(h>0\)を動かした点\(x=t+h\)により、区間\((t,t+h)\)を考えます。そうすると、関数\(f(x)\)と\(x\)軸に囲まれた区間\((t,t+h)\)の面積は、関数\(G(t)\)の定義より、\(G(t+h)-G(t)\)となります。ここで、区間\((t,t+h)\)内の関数\(f(x)\)の最小値を\(m\)、最大値を\(M\)とすると、区間\((t,t+h)\)の面積は最小値を高さとする短冊の面積より大きく、最大値を高さとする短冊の面積よりも小さいので、次の不等式が成り立ちます。
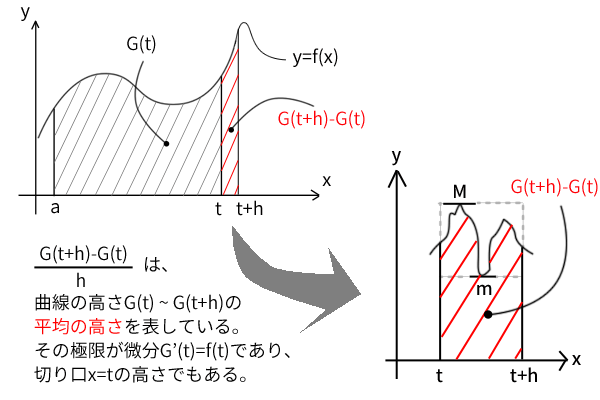
図5:発見!面積の切り口が微分の数式になっている?
\[mh \leq G(t+h)-G(t) \leq Mh\]
したがって、
\[m \leq \frac{G(t+h)-G(t)}{h} \leq M\]
が成り立ちます。ここで、関数\(f(x)\)は連続なので、ある時点の\(m\)よりも\(h\)をより小さく取ることでより大きな\(m\)を取ることができます。逆に、ある時点の\(M\)よりも\(h\)をより小さく取ることでより小さな\(M\)を取ることができます。したがって、\(h\)を小さくしていくと、\(m\)は\(f(t)\)以下でどこまでも大きく、\(M\)は\(f(t)\)以上でどこまでも小さくなることが分かります。つまり、\(h \rightarrow +0\)としたときに、
\[m – f(t) \leq \frac{G(t+h)-G(t)}{h} – f(t) \leq M – f(t)\ \ \ \dots\ \ \ (1)\]
の左右両辺は\(0\)に収束します。
仮に、
\[ \frac{G(t+h)-G(t)}{h} \neq f(t)\]
と左辺が収束したとすると、\(m\)と\(M\)は\(f(t)\)にどこまでも近づくので\(f(t)\)により近い\(m\)または\(M\)が存在してしまうことになり(例えば
\[\frac{ \frac{G(t+h)-G(t)}{h}-f(t)}{2}\]
ほど\(f(t)\)により近づくことができます)、これは数式(1)に矛盾することになります。したがって、
\[ \frac{G(t+h)-G(t)}{h} \rightarrow f(t)\]
つまり、
\[ \lim_{h \rightarrow +0} \frac{G(t+h)-G(t)}{h} = f(t)\]
が成り立ちます。ここで\(t\)は変数なので\(x\)に置き換えてもこの等式は成立します。また、\(h < 0\)の場合も同様に成り立ち、左辺は微分の定義となっているので\(G'(t)\)となり、 \[G'(x)=f(x)\] を証明できました。□
上記の証明は、関数\(f(x)\)と\(x\)軸に囲まれた区間\((a,t)\)という図形の\(x=t\)での切り口の長さが、その図形の面積を表す関数\(G(t)\)を微分した導関数\(G'(t)\)で表されるということを意味します。
このことをより深く理解するには、関数\(G(x)\)を改めて2変数関数として別の平面座標に曲線として下図のように書き直すと良いのです。つまり、図形の面積は単純に数量であり、他の科学の数量を平面座標のグラフとして描くことと何も変わらない作業を行えるということです。
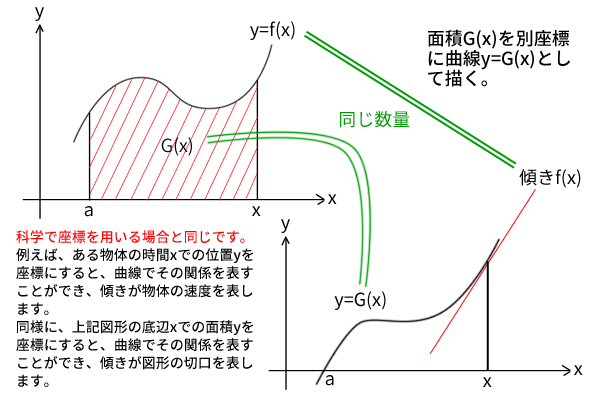
図6:座標の置き直し、面積の微分(切り口)=曲線の微分(傾き)
そうすると、改めて描いた座標においては、関数\(G(x)\)は曲線となり、これを微分して求めた導関数\(G'(x)\)は曲線の傾きとなります。通常、微分というと曲線の傾きを求めることをイメージしますが、数式のうえではこれと同じことを上記の証明は行っていたことが分かります。
両座標の関係を整理すると、数量として「元の座標の関数\(G(x)\)が表す面積」=「別の座標の関数\(G(x)\)が表す曲線への\(x\)軸からの長さ」、「元の座標の導関数\(G'(x)\)が表す切り口の長さ」=「別の座標の導関数\(G'(x)\)が表す傾き」が等しくなっており、前者を微分して後者を出すという同じ関係を持っています。
このことは、数式上の数量の計算と座標上の図形は独立して考えることができること、あるいは逆に、座標によって数式上の数量の計算を座標上の図形と関係付けることができることを示しています。つまり、数式は座標と繋げたり切り離したりできるわけです。
そもそも、これが座標を考え出したデカルトの座標を使う方法・目的でもあるのです。微分積分学は座標上で発見・発展した学問ですので、このような座標の仕組みや効果をきちんと理解しておくことが微分積分学の深い理解を得るための助けになります。座標について、より詳しくは別の記事「図形と方程式とデカルト、高校数学と科学の基礎について」をご覧ください。
この節の最後に、微分積分学の第一基本定理の最も大きな意義を指摘しておきます。それは、原始関数の定義「微分をすると\(f(x)\)になる関数」を振り返っていただいて、関数\(f(x)\)の区間\((a,t)\)で囲まれた面積の関数\(G(x)\)が\(G'(x)=f(x)\)を満たし、原始関数となっていることを証明できたことです。この事実が微分積分学の基本公式の証明へとつながって行きますので、この指摘を記憶に留めておいてください。
微分→積分(微分積分学の第二基本定理)の証明
【微分積分学の第二基本定理】
微分をすると\(f(x)\)になるいずれの関数も、つまり、いずれの原始関数も、ある一つの原始関数を\(F(x)\)として適切な定数\(C\)を取ると、\(F(x)+C\)と表すことができる。
【証明】
\(f(x)\)についてのどの原始関数でも良いのでそれを\(H(x)\)としましょう。そうすると、\(H(x)-F(x)\)も\(x\)が決まると値が定まるので変数\(x\)の関数となります。どちらも原始関数なので微分することができ、
\[(H(x)-F(x))’=H'(x)-F'(x)=f(x)-f(x)=0\]
がすべての\(x\)について成り立つと分かります。さて、\(H(x)-F(x)\)も変数\(x\)の関数でしたが、微分すると常に\(0\)になる2変数関数はどのようなものが考えられるでしょうか。平面座標上で考えてみましょう。
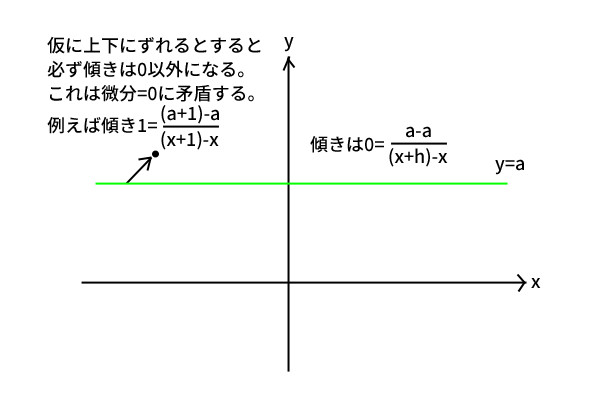
図7:常に傾き0の曲線は定数関数の\(x\)軸に平行な直線しかない。
つまり、2変数関数は\(xy\)平面座標上で曲線を描きます。そして、微分係数は傾きを表します。その傾きが常に\(0\)であるということは、変数\(x\)に対して曲線が上下に動くことがなく\(x\)軸に平行であるということです。\(x\)軸に平行である曲線は、2変数関数ではなく\(y=a\)のような定数の1変数関数しかないと分かります。
したがって、元の関数\(H(x)-F(x)\)も、必要条件として定数の一変数関数でなくてはならないと分かりました。その定数を\(C\)と置くと、
\[H(x)=F(x)+C\]
であることを証明できました。□
さきほどの微分積分学の第一基本定理により、関数\(f(x)\)を積分した関数\(G(x)\)は関数\(f(x)\)の原始関数(\(G'(x)=f(x)\))なのでした。また、この微分積分学の第二基本定理よりすべての原始関数は\(F(x)+C\)と表せるので、関数\(G(x)\)も\(G(x)=F(x)+C\)と表せると分かりました。
そうすると、上記の証明は、関数\(F(x)\)を微分すると関数\(f(x)\)となり、関数\(f(x)\)を積分すると定数を除いて関数\(F(x)+C\)と元に戻ること、つまり、微分→積分が逆演算となっていることを示しています。
これは、原始関数\(F(x)\)ではなく、微分可能な関数\(f(x)\)から微分→積分という演算を行っても同じことです。つまり、座標上で考えると、まず、下図のように関数\(f(x)\)の導関数\(f'(x)\)が傾きを表し、導関数\(f'(x)\)(これも連続とします)を別の座標に2変数関数の曲線として描き直します。
そして、導関数\(f'(x)\)のどの原始関数でも良いのですが原始関数を一つ取ります。例えば、導関数\(f'(x)\)と\(x\)軸と区間\((a,t)\)の面積を\(I(x)\)とおくと、微分積分学の第一定理より\(I(x)\)は関数\(f'(x)\)の原始関数でしたので、ここでは関数\(I(x)\)を一つの原始関数として取りましょう。
そうすると、関数\(f(x)\)と関数\(I(x)\)の差\(f(x)-I(x)\)に対して上記証明と同じ論法を行うことで、\(f(x)=I(x)+C\)を示すことができます。もちろん、これは原始関数\(I(x)\)に限らず、関数\(f'(x)\)のどの原始関数についても一般に成り立ちます。つまり、関数\(f'(x)\)のどの原始関数でも良いので、いずれかの原始関数を\(J(x)\)とすると、\(f(x)=J(x)+C\)が成り立ちます。
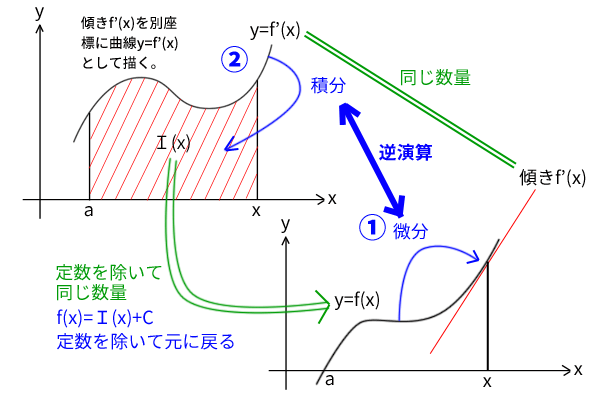
図8:微分→積分は定数を除いて元に戻る逆演算
結局は同じことですが、微分可能な関数\(f(x)\)から考察を開始した方が、微分→積分の逆演算が成り立っていることについては理解しやすいのではないかと思います。
微分積分学の第二基本定理の上記の証明は、定数関数の微分が\(0\)になるという重要な原理を上手く使って微分積分学の第一基本定理でみられたような積分→微分の逆演算についての幾何学的な考察を避けているようにも見えます。微分積分学の第二基本定理における微分→積分の逆演算についての幾何学的な考察もしたいと思いますが、まずは次の微分積分学の基本公式をここまでの二つの定理によって証明してから後述したいと思います。
定積分の公式(微分積分学の基本公式)
【定積分の公式(微分積分学の基本公式)】
\(xy\)平面座標上の連続関数\(y=f(x)\)で表される曲線と\(x\)軸で囲まれた区間\((a,t)\)の図形の面積を表す関数を\(G(t)\)とし、\(G(b)=G(b)-G(a)\)を次の積分記号:
\[G(b)=G(b)-G(a)=\displaystyle \int_a^{b} f(x)dx\]
で表すとする。そうして、関数\(f(x)\)のある一つの原始関数を\(F(x)\)とすると、
\[\displaystyle \int_a^{b} f(x)dx = F(b)-F(a)\]
が成り立つ。

図1再掲:微分積分学の基本公式
【証明】
微分積分学の第一基本定理より、関数\(G'(t)=f(x)\)が成り立つ、つまり、関数\(G(x)\)は原始関数です。したがって、微分積分学の第二基本定理より、いずれの原始関数もある一つの原始関数\(F(x)\)により\(F(x)+C\)と表されるのだから、関数\(G(x)\)も\(G(x)=F(x)+C\)と表されます。
\(x=a\)を代入すると、\(G(a)=0=F(a)+C\)より、\(C=-F(a)\)が成り立ちます。したがって、\(G(b)=F(b)+C=F(b)-F(a)\)が成り立ち、
\[\displaystyle \int_a^{b} f(x)dx = F(b)-F(a)\]
を証明できました。□
これで原始関数「微分をすると\(f(x)\)になる関数」を求めるだけで、複雑な曲線を持つ図形の面積(関数\(G(x)\))を求めることができるようになりました。ちなみに、関数\(G(x)\)の開始点\(x=a\)は定数ですが、制限なく自由に設定できることに注意してください、つまり、区間\((a,b)\)は好きな区間を取れるわけです。
あと、上記公式で求められるのは曲線と\(x\)軸に囲まれた区間の面積ですが、切り貼り、前述した座標の取り方等の工夫次第で様々な図形の面積・体積等を計算できるようになったことも指摘しておきます。
例えば、簡単な放物線\(y=x^2\)の\(x\)軸に囲まれた区間\((1,2)\)の面積を求めるのでも、上記公式を使わずに求めようとするとかなり大変だと思いますが、上記公式を用いれば、微分に慣れていれば「微分をすると\(x^2\)になる関数」はすぐに\(\frac{1}{3}x^3\)だと思いつき、
\[\displaystyle \int_1^{2} x^2 dx = \left[\frac{1}{3}x^3\right]_1^{2} = \frac{8}{3}-\frac{1}{3} = \frac{7}{3} = 2.333\dots\]
と簡単に計算ができてしまいます。そこから分かることは底辺\(1\)、高さ\(2.3\)の四角形よりも大きく、底辺\(1\)、高さ\(2.4\)の四角形よりも小さいなどと直感的ではない事実ではないでしょうか。他のたくさんの関数とその特定区間についても同様なのです。
ここまでで当時の人々の驚きを少し実感できましたでしょうか。多少なりとも実感ができると、様々な図形について出題されるだろう演習問題も格別の興味を持って取り組むことができるのではないかと思います。
微分→積分(微分積分学の第二基本定理)の別証明
それでは、最後に改めて微分積分学の第二基本定理、つまり、関数\(f(x)\)を微分して積分すると\(f(x)+C\)に戻ることを先ほどの証明よりも幾何学的な直観に訴える形の別証明にて示したいと思います。
【微分積分学の第二基本定理(関数\(f(x)\)を中心にした言い換え版)】
微分可能な関数\(f(x)\)の導関数\(f'(x)\)を連続としたとき、\(xy\)平面座標上で曲線\(y=f'(x)\)と\(x\)軸に囲まれた区間\((a,t)\)の面積は、\(f(t)-f(a)\)である。
そして、導関数\(f'(x)\)のいずれの原始関数\(h(x)\)もある一つの原始関数\(g(x)\)により\(h(x)=g(x)+C\)と表される。特に、\(f(x)=g(x)+C\)である。
【微分積分学の第二基本定理の別証明】
さきほど示した図8「微分→積分は定数を除いて元に戻る逆演算」のように、\(xy\)平面座標上で曲線\(y=f(x)\)の傾きを表す導関数\(y=f'(x)\)は、その\(xy\)平面座標から切り離して数を表す数式として単独で考えることができます。さらに、その単独で考えていた関数\(y=f'(x)\)は、別の\(xy\)平面座標に曲線\(y=f'(x)\)として描くことができます。これがデカルト座標の基本的な使い方であることは前述しました。
次に、曲線\(y=f'(x)\)を描いた平面座標において、曲線\(y=f'(x)\)と\(x\)軸に囲まれた区間\((a,t)\)を考えます。この図形の面積が\(f(t)-f(a)\)であることを示すことができたら、前述の「積分→微分(微分積分学の第一基本定理)の証明」内で提示した意味での「積分(下記再掲)」という用語において、関数\(f(x)\)を微分して積分すると\(f(x)+C\)に戻ること、という微分→積分が逆演算であることを示したことになります。なぜなら、定数\(C=-f(a)\)と考えられるからです。
【このページでの積分の定義(再掲)】
通常、高校数学の範囲では、積分するとは原始関数を求めること、あるいは、求めた原始関数より面積\(F(b)-F(a)\)を計算することを意味しますが、ここでは関数\(f(x)\)と\(x\)軸に囲まれた区間\((a,t)\)の面積の関数\(G(t)\)、あるいは、面積\(G(b)-G(a)\)を求めることを指すことにしましょう。
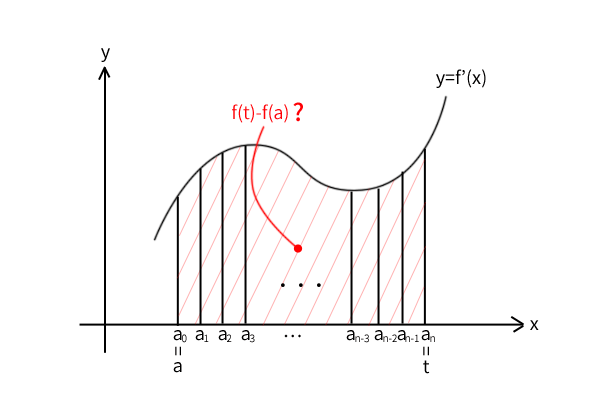
図9:底辺を等分して面積を\(n\)分割
さて、それでは次に上図のように区間\((a,t)\)を\(n\)個の区間\((a=a_0,a_1)\),\((a_1,a_2)\),\((a_2,a_3)\)\(\ \cdots\ \)\((a_{n-3},a_{n-2})\),\((a_{n-2},a_{n-1})\),\((a_{n-1},a_n=t)\)に分割します。各区間の長さは\(h_n=\frac{t-a}{n}\)と等分します。
一方で、面積かまだ分からない関数\(f(x)\)と区間\((a,t)\)についても同様の分割を施すことはできるので、数式\(f(t)-f(a)\)は以下のように変形できます。
\[f(t)-f(a)=f(a_n)-f(a_0)=\sum_{k=0}^{n-1} f(a_{k+1})-f(a_k)=\sum_{k=0}^{n-1} \frac{f(a_{k+1})-f(a_k)}{h_n}\cdot h_n \]
ここで、証明は高校数学の範囲ではできませんが、教科書でも数学Ⅲ第6章「微分法の応用」で紹介されている平均値の定理を用います。平均値の定理を教科書から引用すると、
【平均値の定理】
関数\(f(x)\)が閉区間\([a,b]\)で連続で、開区間\((a,b)\)で微分可能ならば、
\[\frac{f(b)-f(a)}{b-a}=f'(c),\ a < c < b\]
を満たす実数\(c\)が存在する。
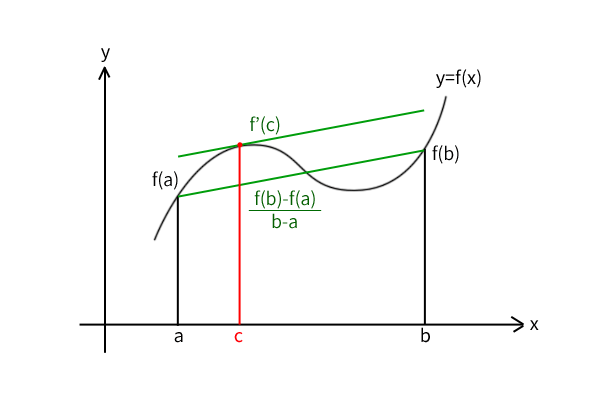
図10:平均値の定理
図を見れば、連続かつ微分可能ならばどこかで同じ傾きになるだろう、と直観的には受け入れやすい定理だと思います。ただ、厳密な証明には詰めなければならない問題点があり、多くのステップが必要になります。
平均値の定理を分割した各区間\((a_k,a_{k+1})\)に適用すると、
\[\frac{f(a_{k+1})-f(a_k)}{h_n}=f'(c_k), a_k < c_k < a_{k+1} \]
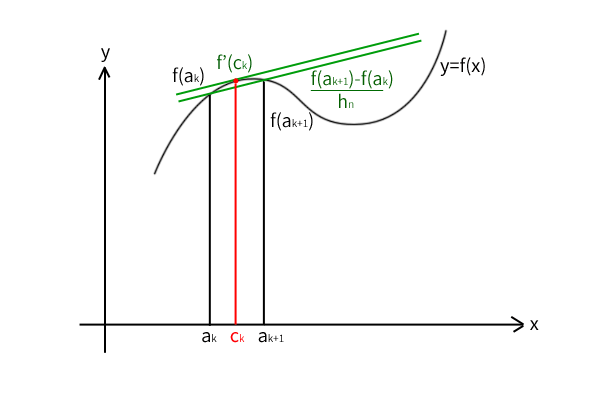
図11:曲線\(y=f(x)\)に平均値の定理を適用した図
ちなみに、平均値の定理を適用した上図は曲線\(y=f'(x)\)の座標ではなく、曲線\(y=f(x)\)の座標であることに注意しましょう。そもそも、関数\(f(x)\)は曲線\(y=f'(x)\)の座標に表れるかどうかもまだ分からないのでした。
この各区間に平均値の定理を適用した式を先ほどの\(f(t)-f(a)\)の変形式に代入すると、
\[f(t)-f(a)=\sum_{k=0}^{n-1} \frac{f(a_{k+1})-f(a_k)}{h_n}\cdot h_n = \sum_{k=0}^{n-1} f'(c_k)\cdot h_n \]
が成り立ちます。ここで、この式はどのような\(n\)に対しても成立することが分かっています。つまり、\(n\)をどれだけ大きくして分割を細かくしても成立しています。各項\(f'(c_k)\cdot h_n\)は下図のように曲線\(y=f'(x)\)の座標上では、底辺\(h_n\)で高さ\(f'(c_k)\)の四角形の面積を表します。
この平均値の定理による変形によって、初めて関数\(f(x)\)と曲線\(y=f'(x)\)に囲まれた区間の面積の関係が見つかったことに注意してください。つまり、区間\((a,t)\)のすべての\(f'(c_k)\)で決まる四角形の面積の和を取ると\(f(t)-f(a)\)になります。ただし、曲線\(y=f'(x)\)に囲まれた区間の面積それ自身ではないので誤差があります。
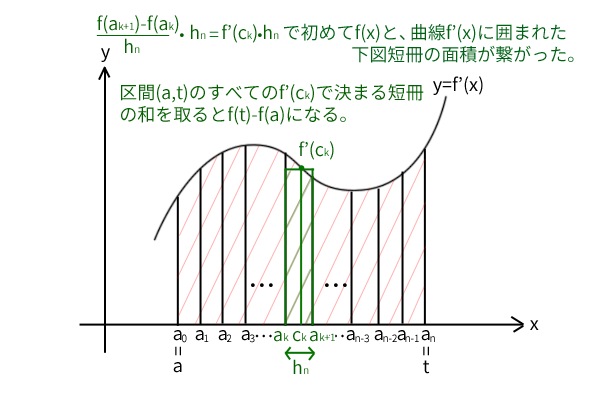
図12:関数\(f(x)\)と曲線\(y=f'(x)\)に囲まれた区間の面積の関係
ここで\(n \rightarrow \infty\)と\(n\)を限りなく大きくして分割を増やしていくと、上式の右辺は曲線\(y=f'(x)\)と\(x\)軸に囲まれた区間\((a,t)\)の面積へと近づいて行くように見えます。実際に近づいていくことを証明できるのですが、何がポイントかというと、各分割の誤差は各点\(c_k\)が各分割区間の内点であること\(a_k < c_k < a_{k+1}\)を常に満たすので、たしかに分割が小さくなるほどに小さくなるでしょう、しかし、それに伴い分割する数\(n\)も増えるので、全体として誤差の和が\(0\)へと収束しするのかは疑問に思えるのです。
仮に、全体として誤差の和が\(0\)へと収束しなければ、曲線\(y=f'(x)\)と\(x\)軸に囲まれた区間\((a,t)\)の面積に限りなく近づいていくとは言えないわけです。一方で、全体として誤差の和が\(0\)へと収束すれば、上式はどんな\(n\)の値でも成立しているので、その収束先は\(f(t)-f(a)\)しかありえず、曲線\(y=f'(x)\)と\(x\)軸に囲まれた区間\((a,t)\)の面積と\(f(t)-f(a)\)は等しいと言え、定理の中盤まで、つまり、微分→積分が逆演算であることまで示せたことになります。
それでは、その詰めの証明に入りたいと思います。まず、微分積分学の第一基本定理の証明を思い出していただき、いくつかの前提を受け入れ、曲線\(y=f'(x)\)と\(x\)軸に囲まれた区間\((a,t)\)の面積を関数\(G(t)\)で表すとします。そうすると、微分積分学の第一基本定理より、関数\(G(t)\)は区間\((a,t)\)で微分可能となり、\(G(t)-G(a)\)に対して\(f(t)-f(a)\)と同様の変形式を施すことができ、
\[G(t)-G(a)=\sum_{k=0}^{n-1} \frac{G(a_{k+1})-G(a_k)}{h_n}\cdot h_n = \sum_{k=0}^{n-1} G'(d_k)\cdot h_n \]
が成り立ちます。その上、やはり微分積分学の第一基本定理より、\(G'(t)=f'(x)\)が成り立ちます。ちなみに、ここでは関数\(G(t)\)は、曲線\(y=f(x)\)ではなく、曲線\(y=f'(x)\)の面積であることに注意してください。くわえて、点\(d_k\)は点\(c_k\)と同じ区間\((a_k, a_{k+1})\)にある異なる点であることにも注意してください。したがって、
\[G(t)-G(a) = \sum_{k=0}^{n-1} f'(d_k)\cdot h_n,\ a_k < d_k < a_{k+1} \]
が成り立ちます。それでは、\(G(t)-G(a)\)と\(f(t)-f(a)\)の差を取ってみましょう。
\[G(t)-G(a)-(f(t)-f(a)) = \sum_{k=0}^{n-1} (f'(d_k)-f'(c_k))\cdot h_n\ \cdots\ (2)\]
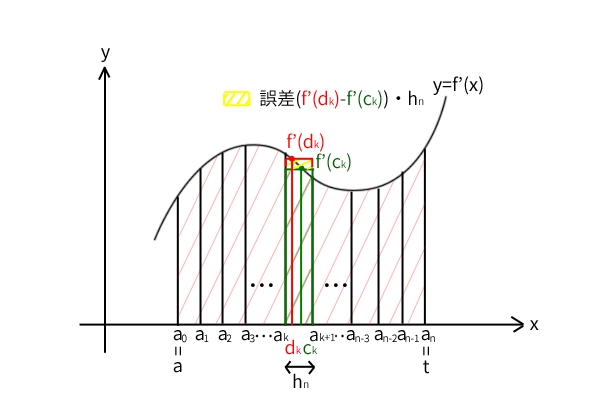
図13:同じ区間に\(f'(d_k)\)と\(f'(c_k)\)が入る
\(G(t)-G(a)\)は曲線\(y=f'(x)\)と\(x\)軸に囲まれた区間\((a,t)\)の面積なのですから、この式から\(f(t)-f(a)\)との誤差を見積もってみたいと思います。そうするとまず、一区間の高さの誤差\(|f'(d_k)-f'(c_k)|\)は\(n\)を限りなく大きくすることでいくらでも小さくできることが分かります(微分積分学の第一基本定理の証明で行った最小値・最大値の議論を思い出してください)。
したがって、逆に、閉区間\([a,t]\)で\(y=f'(x)\)は連続なので、ただ一つのどのように小さな\(\epsilon > 0\)であってもすべての\(n\)個の区間において誤差\(\epsilon > |f'(d_k)-f'(c_k)|\)を満たすような\(n\)が、\(n\)をどこまでも大きく取ることによっていずれかでは、取れるはずです。ここでも\(|f'(d_k)-f'(c_k)|\)の最大値を考えると直観的な理解を助けてくれると思います。最大値が\(\epsilon\)より小さければ他の誤差も小さいはずだからです。あと、区間\([a,t]\)が閉区間であること、これが最大値を取れることを十分に保証してくれています。
まとめると、すべての\(|f'(d_k)-f'(c_k)|\)がとても小さな\(\epsilon > 0\)よりも例外なく小さくなるように\(n\)個の分割を増やしていくということです。曲線\(y=f'(x)\)が閉区間\([a,t]\)で連続なのでゆっくり考えれば直観的には受け入れられる事実かと思いますが、それが必ずできるということは厳密には証明が必要なことです。厳密な証明は、高校数学の範囲では難しいので、残念ですがここでは省略いたします。
そうすると、上式の右辺は以下のような不等式を満たします。ちなみに、一番初めの不等式は三角不等式です。
\[|\sum_{k=0}^{n-1} (f'(d_k)-f'(c_k))\cdot h_n| \leq \sum_{k=0}^{n-1} (|f'(d_k)-f'(c_k)|)\cdot h_n < \sum_{k=0}^{n-1} \epsilon \cdot h_n = h_n \cdot \sum_{k=0}^{n-1} \epsilon = \frac{t-a}{n} \cdot n \epsilon = (t-a) \cdot \epsilon\] ここで\((t-a)\)は固定されていますので、\(\epsilon\)を小さくしていくと上式最右辺\((t-a) \cdot \epsilon\)も限りなく小さくなっていきます。そして、\(\epsilon\)を小さくしていくということは、\(n\)を限りなく大きくして分割を増やすということなので、つまり、\(n\)を限りなく大きくして分割を増やしていくと、
\[\sum_{k=0}^{n-1} (f'(d_k)-f'(c_k))\cdot h_n \rightarrow 0\ (n\rightarrow \infty)\]
と誤差は\(0\)に収束することが分かりました。ここまでは、曲線\(y=f'(x)\)と\(x\)軸に囲まれた区間\((a_k, a_{k+1})\)に着目して仮にあるとすれば全体の誤差は\(n\)に応じてどれくらいに収まるのかを見積もってきましたが、一方で、数式(2)はすべての\(n\)について成り立っています。したがって、仮に\(G(t)-G(a)-(f(t)-f(a)) \neq 0\)であったならば、それよりも小さく右辺が\(0\)に近づくということはできないはずですから、上式と矛盾してしまいます。つまり、\(G(t)-G(a)-(f(t)-f(a)) = 0\)が成り立つことが分かりました。
結局、論法としては誤差を見積もりそれが証明には必要でしたが、すべての\(n\)について\(G(t)-G(a)-(f(t)-f(a)) = 0\)であるという結論が得られたということで、実際にはすべての\(n\)について誤差はそもそもなかったわけです。
ただし、通常この論法は、区間\((a_k, a_{k+1})\)で取る点を平均値の定理で得られた点\(c_k\)ではなく、区間内のいずれか勝手に選んだ点に代えてみると、それでも上記の誤差の見積もりは成立しますので、\(n\)を大きくして分割を進めると勝手に選んだ点であっても多数の四角形の面積の和が面積\(G(t)-G(a)\)に収束するという論法として使われます。
さて、これで\(f(t)-f(a)\)が曲線\(y=f'(x)\)と\(x\)軸に囲まれた区間\((a,t)\)の面積であり、つまり、微分→積分が逆演算であることまでを示せました。
最後に、定理の残りの部分を証明すると、導関数\(f'(x)\)のいずれかの原始関数を\(h(x)\)とすると、原始関数の定義から\(h'(x)=f'(x)\)ですから(\(h(x)\)が\(f(x)\)が満たすべきすべての条件を満たしていることを確認してください)、結局は、ここまで\(f(x)\)について行ってきた議論がまったく同様に成立します。それは、ある一つの原始関数\(g(x)\)についても同様です。したがって、
\[G(t)-G(a)=f(t)-f(a)=h(t)-h(a)=g(t)-g(a) \]
が成り立ちます。変形すると、\(h(t)=g(t)+(-g(a)+h(a))\)となり、\(-g(a)+h(a)\)は定数であり、関数として変数\(t\)を変数\(x\)に置き換えればいずれかの定数\(C\)で、\(h(x)=g(x)+C\)と表されることが分かりました。同様に、\(f(x)=g(x)+C\)も示されました。□
ちなみに、上記証明では、微分積分学の第一基本定理を途中で用いたために微分積分学の基本公式までほぼ証明できています。
まとめ
いかがでしたでしょうか、最後の別証明は少し難しかったかもしれません。ただ、このページの内容を理解すれば、少なくとも高校数学の範囲における微分積分学の要点は掴めたと言えます。
ただ、それのみならず、前回の記事「図形と方程式とデカルト、高校数学と科学の基礎について」と続けて読んで頂ければ、ギリシャなどで発展した数学、特に論理学と幾何学が、インド・アラブなどで発展した数学、特に代数学と、近世ヨーロッパにてデカルトの手によって結合され、その座標上でニュートンが物理学と微分積分学の花を咲かせるという壮大な科学の物語を感じることができるのではないでしょうか。
微分という代数上の極限操作が座標上で複数解釈されることで微分積分学の基本定理は発見され、複雑な図形の面積その他まで代数上の極限操作のみでことごとく計算ができるようになりました。「代数上の極限操作で複雑な図形の面積を容易に計算できる」、この関係はデカルト・ニュートン以前では思いもよらないことでした。まさに数学者や科学者がよく使う言葉ですが、自然の神秘の発見と言ってよいものであり、座標と微分積分学の基本定理の発見は、その後、形作られていく物質文明の号砲であったようにも感じられます。
すでに物質文明の陰と陽は、この数百年の内にも出尽くした感はありますが、このような始まりの歴史と内容を理解すれば、その「物質的」なものですらすべて、人々の知性と手と汗から、個性的な人間であるデカルトやニュートンの思想、それにともなう知識の発見から生まれ出でていることを実感できることだろうと思います。その実感は、これも数学者や科学者がよく使う言葉ですが、自然と人間の対話、そして人間精神の結露たる学問を侮らず、過信せずに学ぼうとする土台となるのではないでしょうか。
以上の入り口を理解すれば、微分積分学、ひいては数学全般が美しく強力な学問であるということも実感されて、さらに奥深い発見がありそうだと予感させてくれるのではないでしょうか。たくさんの胸躍る数学的な発見がこの先に待っています。多くの人が発する雑多な知識に迷うことなく、自分に与えられた感性と理性を信じて探究を進めてください。
その他の参考文献:
「定本 解析概論」 高木貞治著 岩波書店
著者:L&M個別オンライン教室 瀬端隼也
公開日:2022年12月21日
修正日:-



※このサイトはreCAPTCHAによって保護されています。そのためGoogleのPrivacy PolicyとTerms of Serviceが適用されます。