矛盾と背理法について

【目次】
１．背理法の定義と復習
２．矛盾の定義と解説
３．背理法が成り立つ理由
３－１．他の命題も矛盾
３－２．発展：背理法は正しいのか

背理法の定義と復習

まず、背理法の復習をしましょう。

背理法とは、ある命題の否定を仮定するとそれを根拠として矛盾が導かれることを示し、その矛盾を根拠として元の命題が成り立つことを証明する方法です。

普通の証明は、つまり、ある命題が成り立つことを証明するには、他の命題を前提として一つひとつ根拠となる複数の命題の成立を証明して行って、最後に元の命題が成り立つことへ繋げていきます。元の命題の内容は、その過程においてある意味、詳しく解説されることになり、証明があれば元の命題の内容についても深い理解を得られることになります。

一方で、背理法の場合には、ある命題が成り立たないことを出発点とするので、その意味では、通常の証明のゴールがスタートに置き換わっているのです。その上、基本的に、背理法のゴールは矛盾が生まれる他の命題であり、その過程の証明は、ある意味、矛盾を持つ命題の詳しい解説であって、元の命題の理解は必ずしも必要ないという印象すら受けてしまいます。

そこには、ある命題のそれ自体に対する深い理解もなしに、その証明ができたと言ってよいのか、という違和感があると言っても良いかもしれません。

この普通の証明と背理法の違いを何か別の物事でたとえると、例えば自動車の組み立て作業にたとえると良いかもしれません。つまり、ある部品を使うと自動車がきちんと動いたというのが普通の証明で、ある部品とは違う値段の安い部品を代わりに使うと自動車が動かなかったというのが、背理法であると言えます。前者は、自動車の構造を理解していないと組み立てられませんが、後者は、部品を入れ替えるだけで良く、部品自体の構造を理解する必要はありません。良く分からない例えでしょうか、、。

とにかく、このように背理法による証明は、通常の証明とずいぶんと雰囲気が異なるので、なぜ背理法による証明が正しいと言えるのかをきちんと理解することが大切になります。それでは、次に一つひとつその正しさの理由を押さえていきたいと思います。

矛盾の定義と解説

背理法は、ある命題が成り立たないという仮定から別の命題の矛盾を導き出すのですが、この「矛盾が導き出される」ことがポイントで、矛盾が導き出せなければ背理法は成立しないわけです。では、なぜ矛盾が導き出されると元の命題が成り立つのでしょうか。さらに言えば、そもそも、矛盾をするとなぜいけないのでしょうか？

その答えを考えるには、矛盾とは何かをきちんと理解する必要があります。矛盾という言葉の由来は中国の故事にある、どんな楯も破る矛と、どんな矛も通さない楯だと主張して、矛と楯を売る商売人に対して、それならばその矛をその楯に突き立てよ、しからば、どちらかの主張は必ず間違えになる、とお客が論破したという話にちなんでいます。この故事で重要なのは、「主張は必ず間違えになる」というところで、この部分を数学の命題で正確に考えてみましょう。

まず、命題とは、正しいか正しくないかが定まる主張のことで、正しいことを真、正しくないことを偽というのでした（命題についてを参照）。商売人は、命題「どんな楯も破る矛」と命題「どんな矛も通さない楯」が共に真であると主張しているわけです。お客は、その矛をその楯に突き立てると「矛が楯を通さない」か「矛が楯を通すか」のどちらかが起こる、つまり、命題「どんな楯も破る矛」と命題「どんな矛も通さない楯」のどちらかが必ず偽となると主張しているのです。

つまり、命題「どんな楯も破る矛」と命題「どんな矛も通さない楯」のどちらかは分かりませんが、少なくとも一つの命題について、真であると主張しているのに偽になってしまう、突き詰めるとそこがおかしいのです。このようにある一つの命題が正しくもあり、正しくなくもある。真でもあり偽でもあること、これが矛盾の正確な定義となります。

例えば、白い花を赤い花と言った人がいるとしたら、おかしなことを言うなあと思いますが、そこで終わらずに正確に考えると、赤い花は白い花ではないので、白い花を白い花でないと主張していて、上記の矛盾の定義に合致するわけです。このような簡単な例で細かく考えることは馬鹿らしく感じると思いますが、複雑な数学の問題を考えているときに、なんとなくおかしいから、で済ませると大きな間違いに繋がることがあります。最後まできちんと一つの命題が真であり偽であることを確認することが大切になります。

ちなみに、矛盾に限らず、数学の諸々の計算や考え方は、初めは時間がかかってもきちんと正しい手順を踏めるように心がけることが大切だと思います。正しい手順さえ踏めていれば、そのうち繰り返している間にたいして時間や労力を必要とせずに計算や考えを進めることができるようになります。正しいことが何なのかを探究し理解すること、それが分かったらあまり考えずとも使いこなせるまで習熟すること、この２段階の繰り返しが数学には必要だろうと思います。

そこで、矛盾の定義がきちんと理解できて使えているのであれば、論理自体を深く考察する場合やそのことを誰かに説明する必要がある場合などを除いては、強いて細部まで言い立てる必要はないのです。理解して使っていさえすれば、正しいことは曲がりようがありませんから。したがって、教科書などで見かける背理法の証明は、「ある命題が成り立つとすると、矛盾が生じる」で証明を済ませている場合が普通です。どの命題の真偽が両立しているのか、結論として仮定した命題の否定が成り立つことなどは、当たり前に読者が分かることなので省略されます。

背理法が成り立つ理由

話を戻すと、これで矛盾がなぜおかしいのか、ということははっきりと理解できたと思います。一つの命題の真偽が両立するからです。それでは、なぜ矛盾が導き出されると元の命題が成り立つのでしょうか。もちろん、おかしな結論を導き出すような仮定は間違っていると素朴に考えることもできますが、少なくともおかしいと分かっているのが矛盾を生じている命題だけならば、その命題だけを使わなければ良い、とも思いませんでしょうか。

他の命題も矛盾

その答えとしては、そうはいかないということです。なぜなら、ある命題が矛盾すると他の命題も矛盾してしまうからです。例えば、ある命題から他の命題の矛盾が導かれた場合に、元の命題もやはり矛盾してしまうことを次に示しましょう。

命題\(p\)について、\(p\)が成立していないことを仮定する、ということは、\(p\)が偽であることを仮定することと同じ意味です。\(p\)が偽であるならば、\(\overline{p}\)が真であり、\(\overline{p}\)を根拠に推論（命題について：２－２．命題と推論を参照）を命題\(p_{1}\)、命題\(p_{2}\)、命題\(p_{3}\)・・・と進め、ある命題\(p_{n}\)が矛盾したとします。つまり、命題\(p_{n}\)が真でもあり偽でもあることが示されたとします。（下図参照）

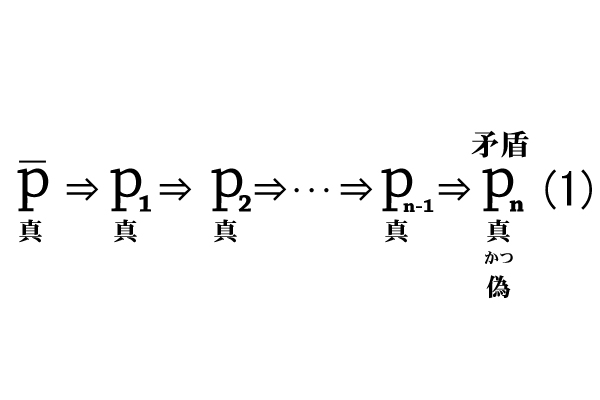
次にまず、命題\(p_{n-1}\ \Rightarrow\ p_{n}\)は成立しているので、その対偶（対偶の証明についてを参照）を取ると命題\(\overline{p}_{n} \Rightarrow\ \overline{p}_{n-1}\)も成立します。ここで、命題\(p_{n}\)は矛盾しているので、偽でもあり、そのため命題\(\overline{p}_{n}\)は真になります。したがって、対偶を用いると命題\(\overline{p}_{n-1}\)は真になるので、命題\(p_{n-1}\)は偽となります。\(\overline{p}\)が真であることと\((1)\)より、命題\(p_{n-1}\)は真でもあるので、命題\(p_{n-1}\)も真偽が両立して矛盾してしまうことになります。

命題\(p_{n-1}\)についても同様に対偶を取って考えると、矛盾が連鎖することが分かり、結果として、\(\overline{p}\)が矛盾することが分かります。（下図参照）

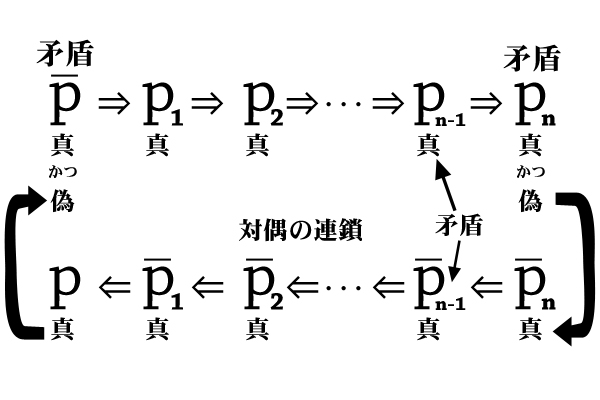
ここまで考えると、矛盾した命題だけを使わなければよいとは言えないこと、さらに仮定した命題自体が矛盾しているので、仮定を撤回しなければならないことがはっきりしたのではないでしょうか。仮定した命題\(\overline{p}\)が偽であると分かったので、元の命題\(p\)が真であること、つまり、命題\(p\)が成り立つことが分かりました。

発展：背理法は正しいのか

少し発展的な内容ですが、仮定した命題\(\overline{p}\)が偽であるからと言って、命題\(p\)が真であることを直ちに認めて良いのかという背理法自体に対する素朴な疑問は残るだろうと思います。例えば、命題\(\overline{p}\)が矛盾したのであるから、命題\(p\)だって矛盾する可能性があるのではないかという指摘もありえます。もしも、実際に命題\(p\)からも矛盾する命題を導くことができたとすると、それは命題\(p\)以外の命題を遡っていったいずれかの命題に、命題\(p\)とも命題\(\overline{p}\)とも両立しえない命題が存在するということを示します。

厳密に考えれば、このような事態も背理法にはありえなくもないと思います。しかし、通常は、それまで成立した命題と、命題\(p\)か命題\(\overline{p}\)のいずれかは矛盾しないということを前提にして背理法を用いるわけです。その前提には、命題\(p\)は真か偽かのいずれかに決まるはずだから、偽でなければ真であり、真でなければ偽と言えるだろうという仮定が潜んでいます。

そこで、もしもすべての前提から証明することのできない命題\(p\)が紛れ込んでしまっていたのであれば、そのような仮定を単純に適用して良いのでしょうか。本当に命題\(p\)は命題として真偽が定まるのか、あるいは、どちらかが矛盾することよりも、どちらかが矛盾しないことを証明する必要の方がありそうな気もします。高校数学で扱う内容については、このようなことを意識する必要はまったくありませんが、難しい内容になってくると様々な可能性を吟味して考える必要が出てきます。

冒頭でも触れましたが、このような背理法の正しさへの問いかけは、数理論理学、数学基礎論、論理学という分野を学んでいくと、より深くその答えを知ることができると思います。そこには、そもそも数学の理論とは何か、命題の証明や正しさ、意味や理解とは何か、という問い掛けが眠っています。

公開日：２０１９年４月４日
修正日：－